Question

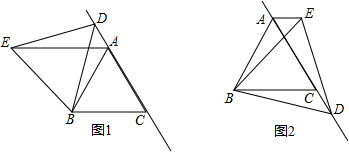
13．等边△ABC中，D是直线AC上的动点，如图①，当D在CA延长线上时，以BD为一边作等边△EDB，连结AE．
（1）△ABE和△BCD会全等吗？请说说你的理由；
（2）试说明AE∥BC的理由；
（3）如图②，当动点D运动到AC的延长线上时，所作△EDB仍为等边三角形，请问是否仍有AE∥BC？说明你的猜想的理由．

Answer 1

分析 （1）首先利用等边三角形的性质得出∠CBD=∠ABE，进而得出△ABE≌△CBD；
（2）利用△ABE≌△CBD，得到∠EAB=∠DCB=60°，又∠ABC=60°，等量代换得到∠EAB=∠ABC，即可解答；
（3）仍有AE∥BC，首先利用等边三角形的性质得出∠CBD=∠ABE，进而得出△ABE≌△CBD，得到∠BAE=∠BCD，利用等边三角形的内角为60°，证明∠EAC=∠ACB，即可解答．

解答 解：（1）∵△ABC和△DBE均为等边三角形，
∴AB=BC，BE=BD，∠ABC=∠EBD=60°，
∵∠CBD=60°-∠ABD，∠ABE=60°-∠ABD，
∴∠CBD=∠ABE，
在△ABE和△CBD中，
$\left\{\begin{array}{l}{AB=CB}\\{∠ABE=∠CBD}\\{BE=BD}\end{array}\right.$，
∴△ABE≌△CBD（SAS）．
（2）∵△ABE≌△CBD，
∴∠EAB=∠DCB=60°，
又∵∠ABC=60°，
∴∠EAB=∠ABC（等量代换），
∴AE∥BC（内错角相等，两直线平行）．
（3）仍有AE∥BC．
∵△ABC和△DBE均为等边三角形，
∴AB=BC，BE=BD，∠ABC=∠EBD=60°，
∵∠CBD=∠ABD-60°，∠ABE=∠ABD-60°，
∴∠CBD=∠ABE，
在△ABE和△CBD中，
$\left\{\begin{array}{l}{AB=CB}\\{∠ABE=∠CBD}\\{BE=BD}\end{array}\right.$，
∴△ABE≌△CBD（SAS），
∴∠BAE=∠BCD，
∵∠ACB=60°，
∴∠BCD=180°-∠ACB=120°，
∴∠BAE=120°，
∵∠BAC=60°，
∴∠EAC=∠BAE-∠BAC=60°，
∴∠EAC=∠ACB，
∴AE∥BC．

点评 此题主要考查了全等三角形的判定与性质，熟练掌握全等三角形的判定方法是解题关键．