题目内容
6. 把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.若AB=6cm,BC=8cm,则线段FG的长为3cm.
把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.若AB=6cm,BC=8cm,则线段FG的长为3cm.
分析 由折叠的性质得到三角形CDG与三角形FDG全等,利用全等三角形对应边相等得到FD=CD,FG=CG,在直角三角形BCD中,利用勾股定理求出BD的长,设FG=x,表示出BG与BF,利用勾股定理列出关于x的方程,求出方程的解即可得到FG的长.
解答 解:由折叠的性质得:△CDG≌△FDG,
∴FD=CD=AB=6cm,FG=CG,
在Rt△BCD中,BC=8cm,CD=AB=6cm,
根据勾股定理得:BD=$\sqrt{{8}^{2}+{6}^{2}}$=10cm,
在Rt△BGF中,设FG=CG=x,则有BG=BC-CG=(8-x)cm,BF=BD-DF=10-6=4cm,
根据勾股定理得:(8-x)2=x2+42,
整理得:-16x+64=16,即16x=48,
解得:x=3,
则FG=3cm,
故答案为:3cm
点评 此题考查了翻折变换(折叠问题),勾股定理,利用了方程的思想,熟练掌握折叠的性质是解本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
3.已知2a2-3a+1的值为9,那么4a2-6a+1的值等于( )
| A. | 17 | B. | 19 | C. | 21 | D. | -19 |
20.下列说法中正确的是( )
| A. | 单项式-x的系数和次数都是1 | B. | 34x3是7次单项式 | ||
| C. | 2πR的系数是2 | D. | 0是单项式 |
15.设a,b是方程x2+x-2013=0的两个实数根,则a2+a+ab的值为( )
| A. | 2013 | B. | 4026 | C. | 1 | D. | 0 |
 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
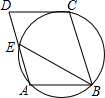 如图,在?ABCD中,过A、B、C三点的圆交AD于E,且与CD相切.若AB=4,BE=5,求DE的长.
如图,在?ABCD中,过A、B、C三点的圆交AD于E,且与CD相切.若AB=4,BE=5,求DE的长. 如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( )
如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( ) 如图,要在高3m,斜坡5m的楼梯表面铺地毯,地毯的长度至少需7m.
如图,要在高3m,斜坡5m的楼梯表面铺地毯,地毯的长度至少需7m.