题目内容
4.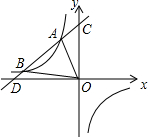 如图,A(-2,m)、B是双曲线y=-$\frac{8}{x}$上两点,直线AB:y=kx+b(k≠0,且k,b为常数)的图象经过点C(0,5),与x轴交于点D.
如图,A(-2,m)、B是双曲线y=-$\frac{8}{x}$上两点,直线AB:y=kx+b(k≠0,且k,b为常数)的图象经过点C(0,5),与x轴交于点D.(1)求直线AB的解析式和点B的坐标;
(2)写出当x取何值时,关于x的不等式kx+b<-$\frac{8}{x}$成立?
(3)求S△AOB.
分析 (1)根据点A在双曲线上,求出m的值,用待定系数法求出直线AB的解析式,运用方程组求出反比例函数与一次函数的交点,得到点B的坐标;
(2)根据图象求出不等式kx+b<-$\frac{8}{x}$的解集;
(3)求出点D的坐标,得到OD的长,根据三角形的面积公式求出S△AOB.
解答 解:(1)∵A(-2,m)在双曲线y=-$\frac{8}{x}$上,
∴m=-$\frac{8}{-2}$=4,
∴A(-2,4),
由题意得,$\left\{\begin{array}{l}{-2k+b=4}\\{b=5}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=5}\end{array}\right.$,
∴直线AB的解析式为:y=$\frac{1}{2}$x+5,
由题意得,$\left\{\begin{array}{l}{y=-\frac{8}{x}}\\{y=\frac{1}{2}x+5}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-8}\\{{y}_{2}=1}\end{array}\right.$,
∴点B的坐标为:(-8,1);
(2)由图象可知,当x<-8或-2<x<0时,不等式kx+b<-$\frac{8}{x}$成立;
(3)y=$\frac{1}{2}$x+5与x轴的交点为(-10,0),
∴OD=10,
∴S△AOB=$\frac{1}{2}$×10×5-$\frac{1}{2}$×10×1-$\frac{1}{2}$×5×2=15.
点评 本题考查的是反比例函数与一次函数的交点,掌握待定系数法求函数解析式和运用方程组求出反比例函数与一次函数的交点是解题的关键.

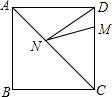 如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )| A. | 6 | B. | 8 | C. | 12 | D. | 10 |
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 等腰梯形 |
 如图,∠2=40°,∠3=100°,∠4=80°,求∠1的度数.
如图,∠2=40°,∠3=100°,∠4=80°,求∠1的度数.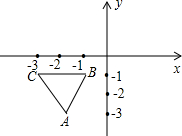 在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移3个单位称为1次变换,如图,已知等边三角形ABC的顶点B,C的坐标分别是(-1,-1),(-3,-1),把△ABC经过连续8次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是(14,-1-$\sqrt{3}$).
在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移3个单位称为1次变换,如图,已知等边三角形ABC的顶点B,C的坐标分别是(-1,-1),(-3,-1),把△ABC经过连续8次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是(14,-1-$\sqrt{3}$).