题目内容
9.△ABC中,D是AB边上的中点,点E,F分别在AC,BC上,你能得到△ADE,△BDF的面积之和与△DEF的面积的大小关系吗?并说明理由.分析 过点B作BG∥AC,交ED的延长线于点G,连接GF,易证△GBD≌△EAD,从而得到DG=DE,S△BDG=S△ADE.由DG=DE可得S△DGF=S△DEF.然后利用S△DGF≤S△BDG+S△BDF就可解决问题.
解答 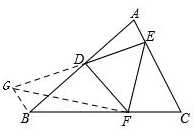 证明:过点B作BG∥AC,交ED的延长线与点G,连接GF,如图所示.
证明:过点B作BG∥AC,交ED的延长线与点G,连接GF,如图所示.
∵BG∥AC,∴∠GBD=∠EAD.
在△GBD和△EAD中,
$\left\{\begin{array}{l}{∠GBD=∠EAD}\\{BD=AD}\\{∠BDG=∠ADE}\end{array}\right.$,
∴△GBD≌△EAD(ASA),
∴DG=DE,S△BDG=S△ADE.
∵DG=DE,∴S△DGF=S△DEF.
∵S△DGF≤S△BDG+S△BDF,
∴S△DEF≤S△ADE+S△BDF.
点评 本题考查了全等三角形的判定与性质、等积变换等知识,当条件中出现中点时,可通过添加平行线,构造全等三角形,实现等量代换.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
19.下列计算正确的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{8}$=4$\sqrt{2}$ | D. | $\sqrt{4}$-$\sqrt{2}$=$\sqrt{2}$ |
19.若( )-(-2)=3,则括号内的数是( )
| A. | -1 | B. | 1 | C. | 5 | D. | -5 |
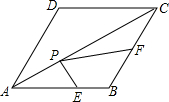 如图,在菱形ABCD中,AB=10,∠DAB=60°,P是对角线AC上一动点,E、F分别是线段AB和BC上的动点,则PE+PF的最小值是5$\sqrt{3}$.
如图,在菱形ABCD中,AB=10,∠DAB=60°,P是对角线AC上一动点,E、F分别是线段AB和BC上的动点,则PE+PF的最小值是5$\sqrt{3}$. 甲从M地出发去N地,乙搭甲的便车也从M地出发到途中与M,N两地在同一条直线上的G地.甲在N地停留一段时间后以110km/h的速度返回,乙在G地停留了$\frac{3}{4}$h后,徒步返回M地,走了5km时与返回的甲相遇并搭甲车返回M地.如图是两人与M地的距离y(单位:km)与行进时间x(单位:h)之间的函数图象(甲、乙均匀速行进,不考虑其他因素).
甲从M地出发去N地,乙搭甲的便车也从M地出发到途中与M,N两地在同一条直线上的G地.甲在N地停留一段时间后以110km/h的速度返回,乙在G地停留了$\frac{3}{4}$h后,徒步返回M地,走了5km时与返回的甲相遇并搭甲车返回M地.如图是两人与M地的距离y(单位:km)与行进时间x(单位:h)之间的函数图象(甲、乙均匀速行进,不考虑其他因素).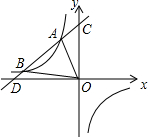 如图,A(-2,m)、B是双曲线y=-$\frac{8}{x}$上两点,直线AB:y=kx+b(k≠0,且k,b为常数)的图象经过点C(0,5),与x轴交于点D.
如图,A(-2,m)、B是双曲线y=-$\frac{8}{x}$上两点,直线AB:y=kx+b(k≠0,且k,b为常数)的图象经过点C(0,5),与x轴交于点D.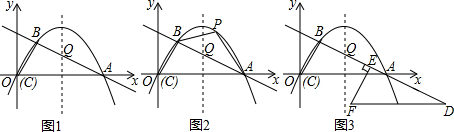
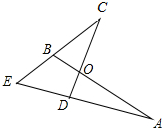 如图,AB交CD于点O,AD、CB的延长线相交于点E,且OA=OC,EA=EC.你能证明∠A=∠C吗?点O在∠AEC的平分线上吗?
如图,AB交CD于点O,AD、CB的延长线相交于点E,且OA=OC,EA=EC.你能证明∠A=∠C吗?点O在∠AEC的平分线上吗?