题目内容
12．
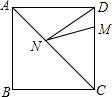如图，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上一动点，则DN+MN的最小值为（ ）| A． | 6 | B． | 8 | C． | 12 | D． | 10 |
分析 要求DN+MN的最小值，DN，MN不能直接求，可考虑通过作辅助线转化DN，MN的值，从而找出其最小值求解．
解答 解：如图，连接BM，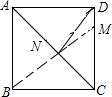
∵点B和点D关于直线AC对称，
∴NB=ND，
则BM就是DN+MN的最小值，
∵正方形ABCD的边长是8，DM=2，
∴CM=6，
∴BM=$\sqrt{{6}^{2}+{8}^{2}}$=10，
∴DN+MN的最小值是10．
故选D．
点评 此题考查正方形的性质和轴对称及勾股定理等知识的综合应用，解题的难点在于确定满足条件的点N的位置：利用轴对称的方法．然后熟练运用勾股定理．
练习册系列答案
备战中考寒假系列答案
相关题目
如图，在长方形ABCD中，已知AB=8cm，BC=10cm，将AD沿直线AF折叠，使点D落在BC的点E处，求CF的长．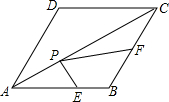
如图，在菱形ABCD中，AB=10，∠DAB=60°，P是对角线AC上一动点，E、F分别是线段AB和BC上的动点，则PE+PF的最小值是5$\sqrt{3}$．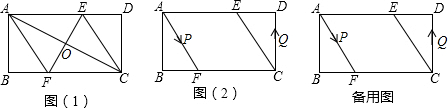
甲从M地出发去N地，乙搭甲的便车也从M地出发到途中与M，N两地在同一条直线上的G地．甲在N地停留一段时间后以110km/h的速度返回，乙在G地停留了$\frac{3}{4}$h后，徒步返回M地，走了5km时与返回的甲相遇并搭甲车返回M地．如图是两人与M地的距离y（单位：km）与行进时间x（单位：h）之间的函数图象（甲、乙均匀速行进，不考虑其他因素）．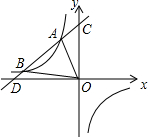
如图，A（-2，m）、B是双曲线y=-$\frac{8}{x}$上两点，直线AB：y=kx+b（k≠0，且k，b为常数）的图象经过点C（0，5），与x轴交于点D．
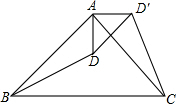如图，△ABC是等腰直角三角形，BC是斜边，将△ABD绕点A逆时针旋转后，能与△ACD′重合．如果AD=2，那么DD′=2$\sqrt{2}$．