题目内容
16.已知二次函数y=x2-(m+3)x+2m-1.(1)证明:无论m取何值时,其图象与x轴总有两个交点;
(2)当其图象与y轴交于点A(0,5)时,求m的值;
(3)设由(2)确定的二次函数的图象与x轴自左向右依次交于点B、C,顶点为D,直线y=kx.
①问是否存在k的值,使得直线y=kx既平分△AOD的面积,又平分它的周长?若存在,求出k的值;若不存在,请说明理由;
②设直线y=kx与AD相交于点P,问是否存在以O、P、A(或D)为顶点的三角形与△OAD相似?若存在,求出P点的坐标;若不存在,请说明理由.
分析 (1)计算出△,可以证明△大于0,即可说明图象与x轴总有两个交点;
(2)将点A(0,5)代入,即可求出m的值;
(3)①可以证明△AOD是以O为顶点的等腰三角形,所以当直线y=kx经过线段AD的中点时即可;
②由①知△AOD是以O为顶点的等腰三角形,只要使OP=AP即可,进而求出P的值.
解答 解:(1)△=(m+3)2-4(2m-1)
=m2-2m+13
=(m-1)2+12>0,
∴无论m取何值时,其图象与x轴总有两个交点;
(2)将点A(0,5)代入可得:2m-1=5,
解得:m=3;
(3)由(2)知m=3,
∴此抛物线的解析式为:y=x2-6x+5,
当y=0时,0=x2-6x+5,解得:x=1或x=5,
∴B(1,0),C(5,0),顶点D(3,-4),
设直线AD的解析式为y=ax+b,将点A(0,5)和点D(3,-4)代入可得:
$\left\{\begin{array}{l}{b=5}\\{3a+b=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-3}\\{b=5}\end{array}\right.$,
∴直线AD的解析式为:y=-3x+5;
①存在,k=$\frac{1}{3}$.
如图,过点D作DV⊥y轴,则:DV=3,OV=3,
∴OD=$\sqrt{{3}^{2}+{4}^{2}}$=5,∴OD=OE,
过点O作OE⊥AD,则E为AD的中点,
过点E作EW⊥y轴,垂足为W,
∴WE∥DV,
∴△AWE∽△AVD,
∴$\frac{AW}{AV}$=$\frac{WE}{DV}=\frac{AE}{AD}$,即:$\frac{AW}{9}$=$\frac{WE}{3}=\frac{1}{2}$,
∴WE=$\frac{3}{2}$,AW=$\frac{9}{2}$,
∴OW=5-$\frac{9}{2}$=$\frac{1}{2}$,
∴点E($\frac{3}{2}$,$\frac{1}{2}$),
把点E代入y=kx,得:
$\frac{1}{2}=\frac{3}{2}k$,
∴k=$\frac{1}{3}$;
②存在点P($\frac{5}{6}$,$\frac{5}{2}$)或P($\frac{13}{6}$,-$\frac{3}{2}$),
设直线AD的解析式为y=kx+b,
将点A(0,5)和点D(3,-4)代入可得:
$\left\{\begin{array}{l}{b=5}\\{3k+b=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-3}\\{b=5}\end{array}\right.$,
∴直线AD的解析式为:y=-3x+5
∵△OAD是等腰三角形,∴当OP=AP时即可,
过点P作PM⊥y轴,垂足为M,则M为OA的中点,
∴OM=$\frac{5}{2}$,
当y=$\frac{5}{2}$时,$-3x+5=\frac{5}{2}$,
解得:x=$\frac{5}{6}$,
∴点P($\frac{5}{6}$,$\frac{5}{2}$)
同理可得P($\frac{13}{6}$,-$\frac{3}{2}$).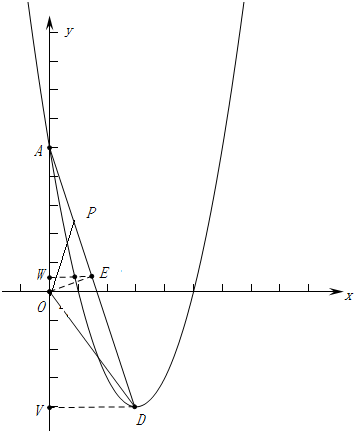
点评 本题主要考查了抛物线与坐标轴的交点问题,以及求一次函数的解析式以及二次函数的解析式的问题,还有二次函数与三角形相似结合的问题,综合性很强,注意总结.

 阅读快车系列答案
阅读快车系列答案| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -5 | … |
| A. | -11 | B. | -2 | C. | 1 | D. | -5 |
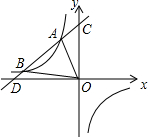 如图,A(-2,m)、B是双曲线y=-$\frac{8}{x}$上两点,直线AB:y=kx+b(k≠0,且k,b为常数)的图象经过点C(0,5),与x轴交于点D.
如图,A(-2,m)、B是双曲线y=-$\frac{8}{x}$上两点,直线AB:y=kx+b(k≠0,且k,b为常数)的图象经过点C(0,5),与x轴交于点D.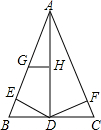 如图,已知AB=AC,AD是中线,BE=CF.
如图,已知AB=AC,AD是中线,BE=CF.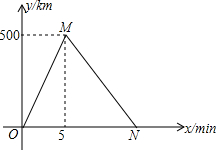 小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象.
小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象. 如图,E是线段CD上的一点,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x-3)2+|y-1|=0.
如图,E是线段CD上的一点,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x-3)2+|y-1|=0.