��Ŀ����
8�����ⱳ������ͼ�٣����ı���ADBC�У���ACB=��ADB=90�㣬AD=BD��̽���߶�AC��BC��CD֮���������ϵ��
С��ͬѧ̽���������˼·�ǣ�����BCD�Ƶ�D����ʱ����ת90�㵽��AED������B��C�ֱ����ڵ�A��E������ͼ�ڣ�����֤��C��A��E��ͬһ��ֱ���ϣ����ҡ�CDE�ǵ���ֱ�������Σ�����CE=$\sqrt{2}$CD���Ӷ��ó����ۣ�AC+BC=$\sqrt{2}$CD��
��Ӧ�ã�
��1����ͼ���У���AC=$\sqrt{2}$��BC=2$\sqrt{2}$����CD=3��
��2����ͼ�ۣ�AB�ǡ�O��ֱ������C��D�ڡ��ϣ�$\widehat{AD}$=$\widehat{BD}$����AB=13��BC=12����CD�ij���
��չ���ɣ�
��3����ͼ�ܣ���ACB=��ADB=90�㣬AD=BD����AC=m��BC=n��m��n������CD�ij����ú�m��n�Ĵ���ʽ��ʾ��
��4����ͼ�ݣ���ACB=90�㣬AC=BC����PΪAB���е㣬����E����AE=$\frac{1}{3}$AC��CE=CA����QΪAE���е㣬���߶�PQ��AC��������ϵ��$\sqrt{2}$PQ=$\frac{1+\sqrt{35}}{6}$AC��$\sqrt{2}$PQ=$\frac{\sqrt{35}-1}{6}$AC��

���� ��1���������֪��AC+BC=$\sqrt{2}$CD�����Խ�AC��BC�ij��ȴ��뼴�ɵó�CD�ij��ȣ�
��2������AC��BD��AD���ɽ�����ת��Ϊ�ڣ�1���ʵ����⣬������Ŀ��������֤��˼·�������CD�ij��ȣ�
��3����ABΪֱ������O������OD���ӳ�����O�ڵ�D1���ɣ�2�������֪��AC+BC=$\sqrt{2}$CD1������ΪCD1=D1D���������ù��ɶ����������CD�ij��ȣ�
��4�����������֪����E��λ�������֣��ֱ��ǵ���E��ֱ��AC���Ҳ�͵���E��ֱ��AC�����ʱ������CQ��CP�����ã�2���ͣ�3���ʵĽ��۽��н��
��� �⣺��1��������֪��AC+BC=$\sqrt{2}$CD��
��$\sqrt{2}$+2$\sqrt{2}$=$\sqrt{2}$CD��
��CD=3�� ��2������AC��BD��AD��
��2������AC��BD��AD��
��AB�ǡ�O��ֱ����
���ADB=��ACB=90�㣬
��$\widehat{AD}=\widehat{BD}$��
��AD=BD��
����BCD�Ƶ�D����ʱ����ת90�㵽��AED������ͼ�ۣ�
���EAD=��DBC��
�ߡ�DBC+��DAC=180�㣬
���EAD+��DAC=180�㣬
��E��A��C���㹲�ߣ�
��AB=13��BC=12��
���ɹ��ɶ�������ã�AC=5��
��BC=AE��
��CE=AE+AC=17��
�ߡ�EDA=��CDB��
���EDA+��ADC=��CDB+��ADC��
����EDC=��ADB=90�㣬
��CD=ED��
���EDC�ǵ���ֱ�������Σ�
��CE=$\sqrt{2}$CD��
��CD=$\frac{17\sqrt{2}}{2}$��
��3��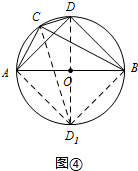 ��ABΪֱ������O������OD���ӳ�����O�ڵ�D1��
��ABΪֱ������O������OD���ӳ�����O�ڵ�D1��
����D1A��D1B��D1C����ͼ��
�ɣ�2����֤�����̿�֪��AC+BC=$\sqrt{2}$D1C��
��D1C=$\frac{\sqrt{2}��m+n��}{2}$��
�֡�D1D�ǡ�O��ֱ����
���DCD1=90�㣬
��AC=m��BC=n��
���ɹ��ɶ�������ã�AB2=m2+n2��
��D1D2=AB2=m2+n2��
��D1C2+CD2=D1D2��
��CD=m2+n2-$\frac{��m+n��^{2}}{2}$=$\frac{��m-n��^{2}}{2}$��
��m��n��
��CD=$\frac{\sqrt{2}��n-m��}{2}$��
��4������E��ֱ��AC�����ʱ����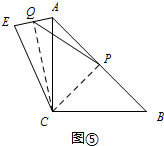 ͼ�ݣ�
ͼ�ݣ�
����CQ��PC��
��AC=BC����ACB=90�㣬
��P��AB���е㣬
��AP=CP����APC=90�㣬
�֡�CA=CE����Q��AE���е㣬
���CQA=90�㣬
��AC=a��
��AE=$\frac{1}{3}$AC��
��AE=$\frac{1}{3}$a��
��AQ=$\frac{1}{2}$AE=$\frac{1}{6}a$��
�ɹ��ɶ�������ã�CQ=$\frac{\sqrt{35}}{6}$a��
�ɣ�2����֤�����̿�֪��AQ+CQ=$\sqrt{2}$PQ��
��$\sqrt{2}$PQ=$\frac{1}{6}$a+$\frac{\sqrt{35}}{6}$a��
��$\sqrt{2}$PQ=$\frac{1+\sqrt{35}}{6}$AC��
����E��ֱ��AC���Ҳ�ʱ����ͼ�ޣ�
����CQ��CP��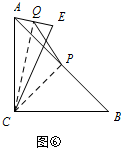 ͬ����֪����AQC=��APC=90�㣬
ͬ����֪����AQC=��APC=90�㣬
��AC=a��
��AQ=$\frac{1}{2}$AE=$\frac{1}{6}a$��
�ɹ��ɶ�������ã�CQ=$\frac{\sqrt{35}}{6}$a��
�ɣ�3���Ľ��ۿ�֪��PQ=$\frac{\sqrt{2}}{2}$��CQ-AQ����
��$\sqrt{2}$PQ=$\frac{\sqrt{35}-1}{6}$AC��
�����������߶�PQ��AC��������ϵ��$\sqrt{2}$PQ=$\frac{1+\sqrt{35}}{6}$AC��$\sqrt{2}$PQ=$\frac{\sqrt{35}-1}{6}$AC��
���� ���⿼��Բ���ۺ����⣬ÿһ�ʶ�������ǰһ�ʵĽ��ۣ��漰���ɶ�����Բ�ܽǶ�������ת�����ʵ�֪ʶ������Ĺؼ��Ǿ����ú���֤���Ľ��������н�𣬿���ѧ���ۺ�����֪ʶ��������

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�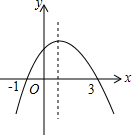 ��ͼ��ʾ�Ƕ��κ���y=ax2+bx+c��a��0����ͼ����������˵����
��ͼ��ʾ�Ƕ��κ���y=ax2+bx+c��a��0����ͼ����������˵������a��0����c��0����4a-b+c��0���ܵ�-1��x��3ʱ��y��0��
������ȷ�ĸ���Ϊ��������
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
| A�� | ��x-$\frac{1}{4}$��2=$\frac{9}{16}$ | B�� | ��x+$\frac{1}{4}$��2=$\frac{9}{16}$ | C�� | ��x-$\frac{1}{2}$��2=$\frac{5}{4}$ | D�� | ��x+$\frac{1}{2}$��2=$\frac{5}{4}$ |
| A�� | 3a3+4a3=7a6 | B�� | 3a2-4a2=-a2 | C�� | 3a2•4a3=12a3 | D�� | ��3a3��2+4a3=$\frac{3}{4}$a2 |
| ָ������ | 21=2 | 22=4 | 23=8 | �� | 31=3 | 32=9 | 33=27 | �� |
| ������ | log22=1 | log24=2 | log28=3 | �� | log33=1 | log39=2 | log327=3 | �� |
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �٢ڢ� |
 ��֪Բ�ĵ���뾶Ϊ5��ĸ�߳�Ϊ8�����Բ�IJ����Ϊ��������
��֪Բ�ĵ���뾶Ϊ5��ĸ�߳�Ϊ8�����Բ�IJ����Ϊ��������| A�� | 80�� | B�� | 40�� | C�� | 105�� | D�� | 65�� |
