题目内容
13.当a、b满足条件a>b>0时,$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1表示焦点在x轴上的椭圆.若$\frac{{x}^{2}}{m+2}$+$\frac{{y}^{2}}{2m-6}$=1表示焦点在x轴上的椭圆,则m的取值范围是3<m<8.分析 根据题意就不等式组,解出解集即可.
解答 解:∵$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1表示焦点在x轴上的椭圆,a>b>0,
∵$\frac{{x}^{2}}{m+2}$+$\frac{{y}^{2}}{2m-6}$=1表示焦点在x轴上的椭圆,
∴$\left\{\begin{array}{l}{2m-6>0}\\{m+2>2m-6}\end{array}\right.$,
解得3<m<8,
∴m的取值范围是3<m<8,
故答案为:3<m<8.
点评 本题考查了解一元一次不等式,能准确的列出不等式组是解题的关键.

练习册系列答案
相关题目
3.下列各图不是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
4.若代数式$\frac{1}{x+2}$有意义,则x的取值范围是( )
| A. | x≠0 | B. | x≠2 | C. | x≠-2 | D. | x>-2 |
1. 如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
 如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )| A. | 62° | B. | 52° | C. | 38° | D. | 28° |
18.我省2013年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2014年增速位居全国第一.若2015年的快递业务量达到4.5亿件.设2014年与2013年这两年的平均增长率为x,则下列方程正确的是( )
| A. | 1.4(1+x)=4.5 | B. | 1.4(1+2x)=4.5 | ||
| C. | 1.4(1+x)2=4.5 | D. | 1.4(1+x)+1.4(1+x)2=4.5 |
5.点M(m+1,m+3)在y轴上,则M点的坐标为( )
| A. | (0,-4) | B. | (4,0) | C. | (-2,0) | D. | (0,2) |
2. 一个长方体的主视图、俯视图如图所示(单位:cm),则其左视图的面积为( )
一个长方体的主视图、俯视图如图所示(单位:cm),则其左视图的面积为( )
 一个长方体的主视图、俯视图如图所示(单位:cm),则其左视图的面积为( )
一个长方体的主视图、俯视图如图所示(单位:cm),则其左视图的面积为( )| A. | 36cm2 | B. | 40cm2 | C. | 90cm2 | D. | 36或40cm2 |
3.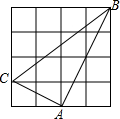 如图,在4×4的正方形网格图中有△ABC,则sin∠ABC=( )
如图,在4×4的正方形网格图中有△ABC,则sin∠ABC=( )
 如图,在4×4的正方形网格图中有△ABC,则sin∠ABC=( )
如图,在4×4的正方形网格图中有△ABC,则sin∠ABC=( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
