题目内容
13.先化简,再求值:$\frac{a-4}{a}$÷($\frac{a+2}{{a}^{2}-2a}$-$\frac{a-1}{{a}^{2}-4a+4}$),其中a=$\sqrt{2}$.分析 先括号内通分化简,然后把乘除化为乘法,最后代入计算即可.
解答 解:原式=$\frac{a-4}{a}$÷[$\frac{{a}^{2}-4}{a(a-2)^{2}}$-$\frac{{a}^{2}-a}{a(a-2)^{2}}$]
=$\frac{a-4}{a}$÷$\frac{a-4}{a(a-2)^{2}}$
=$\frac{a-4}{a}$•$\frac{a(a-2)^{2}}{a-4}$
=(a-2)2,
∵a=$\sqrt{2}$,
∴原式=($\sqrt{2}$-2)2=6-4$\sqrt{2}$
点评 本题考查分式的混合运算化简求值,熟练掌握分式的混合运算法则是解题的关键,通分时学会确定最简公分母,能先约分的先约分化简,属于中考常考题型.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
3.下列算式中,结果等于a6的是( )
| A. | a4+a2 | B. | a2+a2+a2 | C. | a2•a3 | D. | a2•a2•a2 |
4.使二次根式$\sqrt{x-1}$有意义的x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x≤1 | D. | x≥1 |
1.下列分式中,最简分式是( )
| A. | $\frac{{x}^{2}-1}{{x}^{2}+1}$ | B. | $\frac{x+1}{{x}^{2}-1}$ | ||
| C. | $\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-xy}$ | D. | $\frac{{x}^{2}-36}{2x+12}$ |
18.下列一元二次方程没有实数根的是( )
| A. | x2+2x+1=0 | B. | x2+x+2=0 | C. | x2-1=0 | D. | x2-2x-1=0 |
2.某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
| 第1天 | 第2天 | 第3天 | 第4天 | |
| 售价x(元/双) | 150 | 200 | 250 | 300 |
| 销售量y(双) | 40 | 30 | 24 | 20 |
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
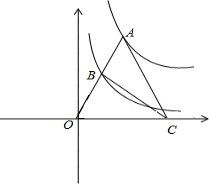 如图,点A为函数y=$\frac{9}{x}$(x>0)图象上一点,连结OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为6.
如图,点A为函数y=$\frac{9}{x}$(x>0)图象上一点,连结OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为6.