题目内容
5.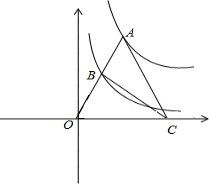 如图,点A为函数y=$\frac{9}{x}$(x>0)图象上一点,连结OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为6.
如图,点A为函数y=$\frac{9}{x}$(x>0)图象上一点,连结OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为6.
分析 根据题意可以分别设出点A、点B的坐标,根据点O、A、B在同一条直线上可以得到A、B的坐标之间的关系,由AO=AC可知点C的横坐标是点A的横坐标的2倍,从而可以得到△ABC的面积.
解答 解:设点A的坐标为(a,$\frac{9}{a}$),点B的坐标为(b,$\frac{1}{b}$),
∵点C是x轴上一点,且AO=AC,
∴点C的坐标是(2a,0),
设过点O(0,0),A(a,$\frac{9}{a}$)的直线的解析式为:y=kx,
∴$\frac{9}{a}=k•a$,
解得,k=$\frac{9}{{a}^{2}}$,
又∵点B(b,$\frac{1}{b}$)在y=$\frac{9}{{a}^{2}}x$上,
∴$\frac{1}{b}=\frac{9}{{a}^{2}}•b$,解得,$\frac{a}{b}=3$或$\frac{a}{b}=-3$(舍去),
∴S△ABC=S△AOC-S△OBC=$\frac{2a•\frac{9}{a}}{2}-\frac{2a•\frac{1}{b}}{2}$=$\frac{18}{2}-\frac{6}{2}=9-3=6$,
故答案为:6.
点评 本题考查反比例函数的图象、三角形的面积、等腰三角形的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
16.某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
| A | B | |
| 进价(万元/套) | 1.5 | 1.2 |
| 售价(万元/套) | 1.65 | 1.4 |
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
20. 如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是( )
如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是( )
 如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是( )
如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是( )| A. | 3 | B. | 2 | C. | 1 | D. | 1.2 |
10. 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )| A. | 65° | B. | 60° | C. | 55° | D. | 45° |
14.算式[-5-(-11)]÷($\frac{3}{2}$×4)之值为何?( )
| A. | 1 | B. | 16 | C. | -$\frac{8}{3}$ | D. | -$\frac{128}{3}$ |
15.在学校开展的“争做最优秀中学生”的一次演讲比赛中,编号1,2,3,4,5的五位同学最后成绩如下表所示:
那么这五位同学演讲成绩的众数与中位数依次是( )
| 参赛者编号 | 1 | 2 | 3 | 4 | 5 |
| 成绩/分 | 96 | 88 | 86 | 93 | 86 |
| A. | 96,88, | B. | 86,86 | C. | 88,86 | D. | 86,88 |