题目内容
18.下列一元二次方程没有实数根的是( )| A. | x2+2x+1=0 | B. | x2+x+2=0 | C. | x2-1=0 | D. | x2-2x-1=0 |
分析 求出每个方程的根的判别式,然后根据判别式的正负情况即可作出判断.
解答 解:A、△=22-4×1×1=0,方程有两个相等实数根,此选项错误;
B、△=12-4×1×2=-7<0,方程没有实数根,此选项正确;
C、△=0-4×1×(-1)=4>0,方程有两个不等的实数根,此选项错误;
D、△=(-2)2-4×1×(-1)=8>0,方程有两个不等的实数根,此选项错误;
故选:B.
点评 本题主要考查一元二次方程根的情况,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
8.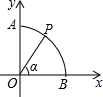 如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
 如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )| A. | (sinα,sinα) | B. | (cosα,cosα) | C. | (cosα,sinα) | D. | (sinα,cosα) |
9.能说明命题“对于任何实数a,|a|>-a”是假命题的一个反例可以是( )
| A. | a=-2 | B. | a=$\frac{1}{3}$ | C. | a=1 | D. | a=$\sqrt{2}$ |
6.抛物线y=2x2-2$\sqrt{2}$x+1与坐标轴的交点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10. 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于$\frac{1}{2}$AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )| A. | 65° | B. | 60° | C. | 55° | D. | 45° |
7.判断2$\sqrt{11}$-1之值介于下列哪两个整数之间?( )
| A. | 3,4 | B. | 4,5 | C. | 5,6 | D. | 6,7 |