题目内容
6. 已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,求证:BF⊥AC.
已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,求证:BF⊥AC.证明:
∵∠AGF=∠ABC(已知)
∴FG∥BC(同位角相等,两直线平行)
∴∠1=∠FBC(两直线平行,內错角相等)
又∵∠1+∠2=180°(已知)
∴∠2+∠FBC=180°(等量代换)
又∵DE⊥AC(已知)
∴∠DEC=∠DEA(垂直的定义)
∴∠BFC=∠DEC=90°(两直线平行,同位角相等)
∴BF⊥AC(垂直的定义)
分析 要证BF⊥AC,只要证得DE∥BF即可,由平行线的判定可知只需证∠2+∠BFC=180°,根据平行线的性质结合已知条件即可求证.
解答 证明:∵∠AGF=∠ABC,
∴BC∥GF(同位角相等,两直线平行),
∴∠1=∠FBC(两直线平行,內错角相等);
又∵∠1+∠2=180°,
∴∠2+∠FBC=180°(等量代换),
∴BF∥DE;
∵DE⊥AC,
∴BF⊥AC,
故答案为同位角相等,两直线平行,两直线平行,內错角相等,∠2+∠FBC=180°,等量代换,∠DEA,垂直的定义,两直线平行,同位角相等,垂直的定义.
点评 本题考查平行线的判定与性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键

练习册系列答案
相关题目
17. 如图,表示下列某个不等式的解集,其中正确的是( )
如图,表示下列某个不等式的解集,其中正确的是( )
 如图,表示下列某个不等式的解集,其中正确的是( )
如图,表示下列某个不等式的解集,其中正确的是( )| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤-2 |
14.菱形具有而矩形不一定具有的性质是( )
| A. | 对角相等 | B. | 每条对角线平分一组对角 | ||
| C. | 对角线互相平分 | D. | 对边平行且相等 |
 如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,若$\frac{3}{2}$∠BOD=∠DOE.
如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,若$\frac{3}{2}$∠BOD=∠DOE. 如图,菱形ABCD的对角线长分别为a,b,以菱形ABCD各边的中点为顶点作四边形A1B1C1D1,然后再以四边形A1B1C1D1各边的中点为顶点作四边形A2B2C2D2,…,如此下去,可得到四边形A2014B2014C2014D2014,它的面积用含a,b的代数式表示为$\frac{1}{{2}^{2015}}$ab.
如图,菱形ABCD的对角线长分别为a,b,以菱形ABCD各边的中点为顶点作四边形A1B1C1D1,然后再以四边形A1B1C1D1各边的中点为顶点作四边形A2B2C2D2,…,如此下去,可得到四边形A2014B2014C2014D2014,它的面积用含a,b的代数式表示为$\frac{1}{{2}^{2015}}$ab.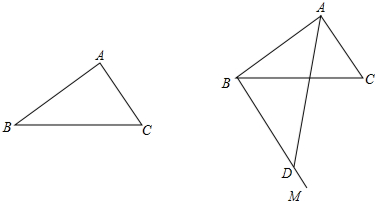
 如图所示,⊙O是△ABC 的外接圆,AB是直径,∠ABC=30°,点E是OC的中点,连接AE并延长交⊙○于点D,连接OD,CD,BD.
如图所示,⊙O是△ABC 的外接圆,AB是直径,∠ABC=30°,点E是OC的中点,连接AE并延长交⊙○于点D,连接OD,CD,BD. 如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O,求证:△ABC≌△DCB.
如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O,求证:△ABC≌△DCB.