题目内容
1. 如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,若$\frac{3}{2}$∠BOD=∠DOE.
如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,若$\frac{3}{2}$∠BOD=∠DOE.(1)求∠BOF的度数;
(2)请写出图中与∠BOD相等的所有的角.
分析 (1)由垂线的定义得出∠BOF=90°即可;
(2)由角平分线和已知条件得出∠BOD=45°,再由垂线的定义和对顶角相等即可得出与∠BOD相等的所有的角.
解答 解:(1)∵FO⊥AB,∴∠BOF=90°;
(2)∵OE平分∠AOD,$\frac{3}{2}$∠BOD=∠DOE,
∴2∠DOE+∠BOD=180°,
即4∠BOD=180°,
∴∠BOD=45°,
∵FO⊥AB,
∴∠AOF=90°,
∵∠AOC=∠BOD=45°,
∴∠COF=90°-45°=45°,
即图中与∠BOD相等的所有的角为∠AOC、∠COF.
点评 本题考查了垂线的定义、角平分线的定义、邻补角、对顶角相等的性质;熟练掌握垂线的定义和对顶角相等的性质是解决问题的关键.

练习册系列答案
相关题目
13.下列计算中,正确的是( )
| A. | 2a3(-a2)=-2a5 | B. | (a-b)2=a2-b2 | C. | (-a)5÷(-a)2=a3 | D. | (-3)-1=3 |
12.矩形具有而一般的平行四边形不一定具有的特征( )
| A. | 对角相等 | B. | 对角线互相平分 | C. | 对角线相等 | D. | 对边相等 |

 已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,求证:BF⊥AC.
已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,求证:BF⊥AC. 如图,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则彩带最短要用10m.
如图,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则彩带最短要用10m.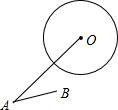 如图,⊙O的半径为1,OA=2.5,∠OAB=30°,则AB与⊙O的位置关系是相离.
如图,⊙O的半径为1,OA=2.5,∠OAB=30°,则AB与⊙O的位置关系是相离.