题目内容
11. 如图,菱形ABCD的对角线长分别为a,b,以菱形ABCD各边的中点为顶点作四边形A1B1C1D1,然后再以四边形A1B1C1D1各边的中点为顶点作四边形A2B2C2D2,…,如此下去,可得到四边形A2014B2014C2014D2014,它的面积用含a,b的代数式表示为$\frac{1}{{2}^{2015}}$ab.
如图,菱形ABCD的对角线长分别为a,b,以菱形ABCD各边的中点为顶点作四边形A1B1C1D1,然后再以四边形A1B1C1D1各边的中点为顶点作四边形A2B2C2D2,…,如此下去,可得到四边形A2014B2014C2014D2014,它的面积用含a,b的代数式表示为$\frac{1}{{2}^{2015}}$ab.
分析 根据三角形中位线定理,逐步推理出各小长方形的面积,总结出规律,用规律解答即可.
解答 解:∵四边形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四边形ABCD=$\frac{1}{2}$ab;
由三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半,
∴四边形A2014B2014C2014D2014的面积为:$\frac{1}{{2}^{2015}}$ab,
故答案为:$\frac{1}{{2}^{2015}}$ab.
点评 本题考查的是菱形的性质及三角形中位线定理的理解及运用,灵活运用定理,注意数形结合思想的应用是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
1.将一元二次方程3(x+1)2-3x=4x2-7x+1化为ax2+bx+c=0(a≠0),则a,b,c分别是( )
| A. | -1,10,2 | B. | 7,10,2 | C. | -1,13,2 | D. | -1,10,4 |
2.下列命题中,错误的是( )
| A. | 矩形的对角线互相平分且相等 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 四个角都相等的四边形是矩形 | |
| D. | 两组对边分别相等的四边形是平行四边形 |
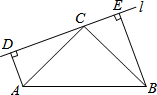 如图,在Rt△ABC中,∠ACB=90°,AC=BC,过C点作直线l,点 D,E在直线l上,连接AD,BE,∠ADC=∠CEB=90°.求证:△ADC≌△CEB.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,过C点作直线l,点 D,E在直线l上,连接AD,BE,∠ADC=∠CEB=90°.求证:△ADC≌△CEB. 已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,求证:BF⊥AC.
已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,求证:BF⊥AC. 小明所在数学兴趣小组,计划用尺规作图作直角三角形,且这个直角三角形的一条边为2倍的单位长度,另一条边为4倍的单位长度.
小明所在数学兴趣小组,计划用尺规作图作直角三角形,且这个直角三角形的一条边为2倍的单位长度,另一条边为4倍的单位长度. 将一副直角三角板ABC和ADE如图放置(其中∠B=60°,∠E=45°),已知DE与AC交于点F,AE∥BC,则∠AFD的度数为75°.
将一副直角三角板ABC和ADE如图放置(其中∠B=60°,∠E=45°),已知DE与AC交于点F,AE∥BC,则∠AFD的度数为75°.