题目内容
3.平移、旋转、翻折是几何图形的最基本的三种图形变换,利用图形变换可将分散的条件相对集中,以达到解决问题的目的.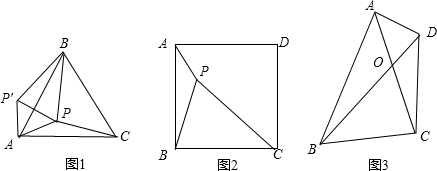
(1)探究发现
如图(1),P是等边△ABC内一点,PA=3,PB=4,PC=5.求∠APB的度数.
解:将△APC绕点A旋转到△APB′的位置,连接PP′,则△APP′是等边三角形.
∵PP′=PA=3,PB=4,PB′=PC=5,
∴P'P2+PB2=P'B2∴△BPP′为直角三角形.∴∠APB的度数为150°.
(2)类比延伸
在正方形ABCD内部有一点P,连接PA、PB、PC,若PA=2,PB=4,∠APB=135°,求PC的长;
(3)拓展迁移
如图(3),在四边形ABCD中,线段AD与BC不平行,AC=BD=a,AC与BD交于点O,且∠AOD=60°,比较AD+BC与a的大小关系,并说明理由.
分析 (1)将△BPC绕点B逆时针旋转60°得△BEA,根据旋转的性质得BE=BP=4,AE=PC=5,∠PBE=60°,则△BPE为等边三角形,得到PE=PB=4,∠BPE=60°,在△AEP中,AE=5,AP=3,PE=4,根据勾股定理的逆定理可得到△APE为直角三角形,且∠APE=90°,即可得到∠APB的度数;
(2)把△ABP绕点B顺时针旋转90°得到△BCP′,根据旋转变换只改变图形的位置不改变图形的形状可得P′B=PB,P′C=PA,然后求出△BPP′是等腰直角三角形,根据等腰直角三角形的性质求出PP′,∠PP′B=45°,再求出∠PP′C=90°,然后利用勾股定理列式计算即可得解;
(3)以AC为边向左做等边三角形PAC,连接PB,证明四边形PABD是平行四边形,再利用三角形三边关系证明即可.
解答 解:将△APC绕点A旋转到△APB′的位置,连接PP′,则△APP′是等边三角形.
∵PP′=PA=3,PB=4,PB′=PC=5,
∴P'P2+PB2=P'B2,
∴△BPP′为直角三角形,
∴∠APB的度数为90°+60°=150°
故答案为:等边;直角;150°
(2)如图1,把△ABP绕点B顺时针旋转90°得到△BCP′,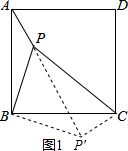
则P′B=PB=4,P′C=PA=2,
∵旋转角是90°,
∴∠PBP′=90°,
∴△BPP′是等腰直角三角形,
∴PP′=$\sqrt{2}$PB=4$\sqrt{2}$,∠PP′B=45°,
∵∠APB=135°,
∴∠CP′B=∠APB=135°,
∴∠PP′C=135°-45°=90°,
在Rt△PP′C中,由勾股定理得,PC=$\sqrt{PP{'}^{2}+P'{C}^{2}}=\sqrt{(4\sqrt{2})^{2}+{2}^{2}}$=6;
(3)AD+BC>a,理由如下:
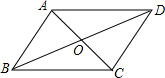
如图2所示,以AC为边向左做等边三角形PAC,连接PB,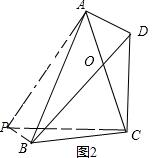
则PA=PC=AC=BD=a,∠PAC=60°,
∵∠AOD=60°,
∴PA∥BD,
∴四边形APBD是平行四边形,
∴AD=PB,
在△PBC中,可得:PB+BC>PC,即AD+BC>a.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等边三角形的判定与性质以及勾股定理的逆定理.

| A. | 对角线互相垂直且平分的四边形是正方形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 四个角相等的四边形是矩形 | |
| D. | 一组对边平行另一组对边相等的四边是平行四边形 |
 如图,在四边形ABCD中,对角线AC、BD相交于点O,∠ADB=∠CBD,AD=BC.
如图,在四边形ABCD中,对角线AC、BD相交于点O,∠ADB=∠CBD,AD=BC.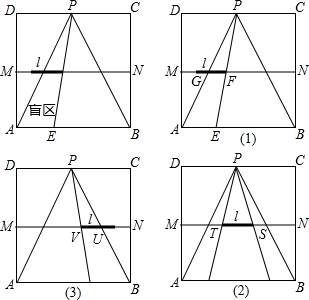
 在下面的正方形网格中,每个小正方形的边长都是1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个三角形,使三边长分别为3,$\sqrt{10}$,5,并求此三角形的面积.
在下面的正方形网格中,每个小正方形的边长都是1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个三角形,使三边长分别为3,$\sqrt{10}$,5,并求此三角形的面积.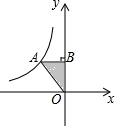 如图,已知A点是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,AB⊥y轴于B,且△AOB的面积为3,则k的值为-6.
如图,已知A点是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,AB⊥y轴于B,且△AOB的面积为3,则k的值为-6.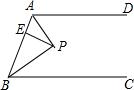 如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为( )
如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为( )