题目内容
11.如图,正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点.现从点P观察线段AB,当长度为1的线段l(图中的黑粗线)以每秒1个单位长的速度沿线段MN从左向右运动时,l将阻挡部分观察视线,在△PAB区域内形成盲区.设l的右端点运动到M点的时刻为0,用t(秒)表示l的运动时间.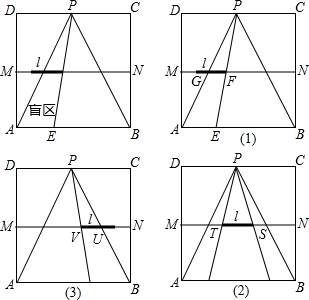
(1)请你针对图(1)(2)(3)中l位于不同位置的情形分别画出在△PAB内相应的盲区,并在盲区内涂上阴影.
(2)设△PAB内的盲区面积是y(平方单位),在下列条件下,求出用t表示y的函数关系式.
①1≤t≤2.
②2≤t≤3.
③3≤t≤4.
根据①~③中得到的结论,请你简单概括y随t变化而变化的情况.
分析 (1)根据题意涂上阴影即可;
(2)根据正方形的性质得AM=2,盲区为梯形,且上底为下底的一半,高为2,然后分段计算:梯形的上底、下底,然后根据梯形的面积分别计算出三中情况下的梯形的面积即可;根据一次函数的性质求解.
解答 解 (1)如图: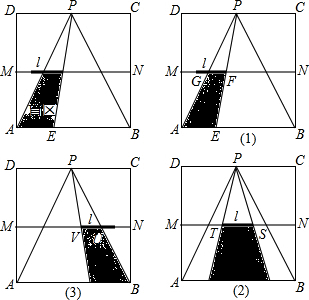 .
.
(2)①当1≤t≤2时,△PAB内的盲区是梯形AEFG.
FG是△PAE的中位线,FG=t-1,AE=2(t-1).而梯形AEFG的高为2,
∴y=$\frac{1}{2}$[(t-1)+2(t-1)]×2=3t-3.
②当2≤t≤3时,△PAB内的盲区是梯形QRST.
易知TS=1,QR=2,而梯形QRST的高为2,
∴y=$\frac{1}{2}$(1+2)×2=3.
③当3≤t≤4时,△PAB内的盲区是梯形WBUV.
易知UV=1-(t-3)=4-t,WB=2(4-t),而梯形的高为2,∴y=$\frac{1}{2}$[(4-t)+2(4-t)]×2=12-3t.
当1≤t≤2时,盲区的面积由0逐渐增大到3;
当2≤t≤3时,盲区的面积y为定值3;
当3≤t≤4时,盲区的面积由3逐渐减小到0.
点评 本题考查了视点、视角和盲区:把观察者所处的位置定为一点,叫视点.人眼到视平面的距离视固定的(视距),视平面左右两个边缘到人眼的连线得到的角度就是视角.视线到达不了的区域为盲区

练习册系列答案
相关题目
1.一个n边形的内角和比它的外角和至少大120°,则n的最小值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |

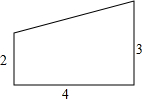 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.
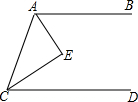 如图,AB∥CD,∠BAC的平分线和∠ACD的平分线交于点E,则AE与CE的位置关系是互相垂直.
如图,AB∥CD,∠BAC的平分线和∠ACD的平分线交于点E,则AE与CE的位置关系是互相垂直.