题目内容
1.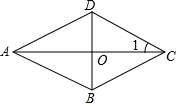 如图,四边形ABCD是菱形,∠1=30°,BD=8cm,求:
如图,四边形ABCD是菱形,∠1=30°,BD=8cm,求:(1)∠ABC的度数;
(2)AB及AC的长.
分析 (1)根据菱形的性质得出∠ADC=2∠CDO,∠ABC=∠ADC,∠DOC=90°,求出∠CDO,即可求出答案;
(2)求出DO,解直角三角形求出DC、OC,即可求出答案.
解答 解:(1)∵四边形ABCD是菱形,
∴∠ADC=2∠CDO,∠ABC=∠ADC,DB⊥AC,
∴∠DOC=90°,
∵∠1=30°,
∴∠CDO=60°,
∴∠ABC=∠ADC=2∠CDO=120°;
(2)∵四边形ABCD是菱形,BD=8cm,
∴DO=BO=4cm,
∵∠DOC=90°,∠1=30°,
∴DC=2DO=8cm,OC=$\sqrt{3}$DO=4$\sqrt{3}$cm;
∵四边形ABCD是菱形,
∴AB=DC=8cm,AC=2OC=8$\sqrt{3}$cm.
点评 本题考查了菱形的性质和解直角三角形等知识点,能灵活运用菱形的性质进行推理是解此题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
16.方程x2+xy+y2=3(x+y)的整数解有( )
| A. | 3组 | B. | 4组 | C. | 5组 | D. | 6组 |
 如图,数轴上表示1、$\sqrt{2}$的对应点分别为A、B,点C为点B关于点A的对称点,设点C所表示的数为x.
如图,数轴上表示1、$\sqrt{2}$的对应点分别为A、B,点C为点B关于点A的对称点,设点C所表示的数为x. 如图,一次函数y=ax-2(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二象限的点,且与x轴、y轴分别交于点C、D.已知tan∠AOC=$\frac{1}{3}$,AO=$\sqrt{10}$.
如图,一次函数y=ax-2(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二象限的点,且与x轴、y轴分别交于点C、D.已知tan∠AOC=$\frac{1}{3}$,AO=$\sqrt{10}$. 如图,O为Rt△ABC的直角边AC上一点,以OC为半径的半圆与斜边AB相切于点D,交AC于点E,已知AB=5,AC=4,求BD的长和⊙O的半径.
如图,O为Rt△ABC的直角边AC上一点,以OC为半径的半圆与斜边AB相切于点D,交AC于点E,已知AB=5,AC=4,求BD的长和⊙O的半径.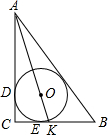 若⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点K,AC=4,CK=1,求内切圆的半径.
若⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点K,AC=4,CK=1,求内切圆的半径.