题目内容
11．
如图，数轴上表示1、$\sqrt{2}$的对应点分别为A、B，点C为点B关于点A的对称点，设点C所表示的数为x．（1）写出实数x的值；
（2）求（x+$\sqrt{2}$）2的值．
分析 （1）根据线段中点的性质，可得答案；
（2）根据代数之求职，可得答案．
解答 解：（1）由数轴上表示1、$\sqrt{2}$的对应点分别为A、B，点C为点B关于点A的对称点，得
$\frac{x+\sqrt{2}}{2}$=1，解得
$x=2-\sqrt{2}$，
（2）当x=2-$\sqrt{2}$时，（x+$\sqrt{2}$）2=4．
点评 本题考查了实数与数轴，利用线段中点的性质是解题关键．
练习册系列答案
相关题目
如图，∠ABD=∠ACD，∠ADB=90°-$\frac{1}{2}$∠BDC，求证：△ABC是等腰三角形．
19．15吨减去它的$\frac{1}{5}$后，再加上$\frac{1}{5}$吨，结果是（ ）
| A． | 15吨 | B． | 12$\frac{1}{5}$吨 | C． | 15$\frac{1}{5}$吨 | D． | 3$\frac{1}{5}$吨 |
6．Word文本中的图形，在图形格式中大小菜单下显示有图形的绝对高度和绝对宽度，同一个图形随其放置方向的变化，所显示的绝对高度和绝对宽度也随之变化．如图①、②、③是同一个三角形以三条不同的边水平放置时，它们所显示的绝对高度和绝对宽度如下表，现有△ABC，已知AB=AC，当它以底边BC水平放置时（如图④），它所显示的绝对高度和绝对宽度如下表，那么当△ABC以腰AB水平放置时（如图⑤），它所显示的绝对高度和绝对宽度分别是（ ）
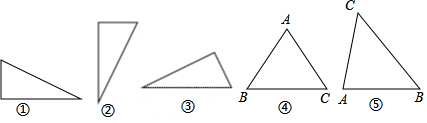
| 图形 | 图① | 图② | 图③ | 图④ | 图⑤ |
| 绝对高度 | 1.50 | 2.00 | 1.20 | 2.40 | ？ |
| 绝对宽度 | 2.00 | 1.50 | 2.50 | 3.60 | ？ |
| A． | 3.60和2.40 | B． | 2.56和3.00 | C． | 2.56和2.88 | D． | 2.88和3.00 |
如图，A、B两城市相距80km，现计划在这两座城市间修建一条高速公路（即线段AB），经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上，已知森林保护区的范围在以P点为圆心，50km为半径的圆形区域内，请问计划修建的这条高速公路会不会穿越保护区，为什么？（参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）
如图，点A是第一象限内的点，坐标为（4，y），OA与x轴正半轴的夹角α的正弦角α的正弦值为$\frac{3}{5}$，求点A的坐标及α的余弦值．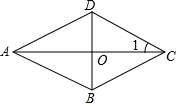
如图，四边形ABCD是菱形，∠1=30°，BD=8cm，求：