题目内容
13．若点O为△ABC的外心，且∠AOC=120°，则∠B=60°或120°．分析 分点B在优$\widehat{AC}$上和点B在劣$\widehat{AC}$上两种情况讨论，根据圆周角定理和圆内接四边形的性质解答即可．
解答 解：当点B在优$\widehat{AC}$上时，
∠ABC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×120°=60°；
当点B在劣$\widehat{AC}$上时，
∠ABC=180°-60°=120°．
故答案为：60°或120°．
点评 本题考查的是圆周角定理和圆内接四边形的性质，掌握一条弧所对的圆周角是它所对的圆心角的一半和圆内接四边形对角互补是解题的关键．
练习册系列答案
相关题目
如图，点A是第一象限内的点，坐标为（4，y），OA与x轴正半轴的夹角α的正弦角α的正弦值为$\frac{3}{5}$，求点A的坐标及α的余弦值．
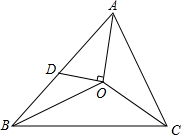如图，O是△ABC的三条角平分线的交点，过点O作AO的垂线交AB于点D，求证：△OBD∽△CBO．
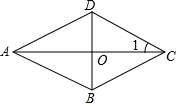如图，四边形ABCD是菱形，∠1=30°，BD=8cm，求：
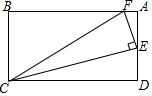已知，如图，在矩形ABC中．E是AD的中点，EF⊥EC交AB于点F，连FC（AB＞AE），求证：$\frac{DE}{AB}$=$\frac{AF}{DE}$．
如图，三条直线两两相交于点A，B，C，图中有12对同位角，有6对内错角，有6对同旁内角．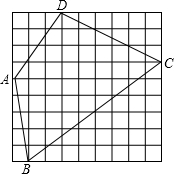
如图，小方格都是边长为1的正方形，求四边形ABCD的周长．
已知：如图，半径都是5cm的两等圆⊙O1和⊙O2相交于点A，B，过A作⊙O1的直径AC与⊙O2交于点D，且AD：DC=3：2，E为DC的中点．