题目内容
15. 如图所示,反比例函数y1=$\frac{6}{x}$的图象与一次函数y2=kx+b的图象交于点A(3,m),B(n,-3),一次函数图象与y轴交于点C.
如图所示,反比例函数y1=$\frac{6}{x}$的图象与一次函数y2=kx+b的图象交于点A(3,m),B(n,-3),一次函数图象与y轴交于点C.(1)求m,n的值;
(2)直接写出y1>y2时自变量x的取值范围;
(3)求△AOC的面积.
分析 (1)把A的坐标代入反比例函数的解析式求出m的值,把B的坐标代入反比例函数解析式求出n的值即可;
(2)结合图象和A、B的坐标即可求出答案;
(3)先把A、B的坐标代入y2=kx+b,利用待定系数法求出一次函数的解析式,再求出点C的坐标,进而得到△AOC的面积.
解答 解:(1)∵反比例函数y1=$\frac{6}{x}$的图象经过点A(3,m),B(n,-3),
∴m=$\frac{6}{3}$=2,-3=$\frac{6}{n}$,
∴m=2,n=-2;
(2)由图象可知,y1>y2时x<-2或0<x<3;
(3)∵一次函数y2=kx+b的图象经过A、B点,
∴$\left\{\begin{array}{l}{3k+b=2}\\{-2k+b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$.
故一次函数的解析式为y=x-1,
∴当x=0时,y=-1,
∴△AOC的面积=$\frac{1}{2}$×1×3=$\frac{3}{2}$.
点评 本题考查了用待定系数法求一次函数的解析式,一次函数与反比例函数图象上点的坐标特征,三角形的面积,一次函数与反比例函数的交点问题的应用,数形结合思想的应用,主要考查学生运用性质进行计算的能力,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
相关题目
20.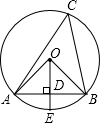 如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )
如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )
 如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )
如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )| A. | ∠ACB=∠AOE | B. | AD=BD | C. | S△AOB=$\frac{1}{2}$S△ABC | D. | AE=BE |
 把一个含有45°角的三角板放在如图所示的两平行线上,测得∠α=120°,则∠β的度数为75°.
把一个含有45°角的三角板放在如图所示的两平行线上,测得∠α=120°,则∠β的度数为75°.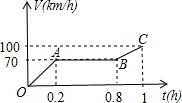 一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法:
一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法: