题目内容
3.计算:$\root{3}{0.001}$-$\sqrt{\frac{1}{100}}$+(-1)3×$\root{2}{(-0.01)^{2}}$.分析 根据立方根、平方根、乘方的定义解答.
解答 解:原式=0.1-$\frac{1}{10}$-1×0.01=-0.01.
点评 本题考查了实数的运算,熟练掌握立方根、平方根是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
8.平面上有n个点(n≥2)且任意三个点不在同一直线上,过这些点中的任两点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可作出3条直线;当有4个点时,可作出6条直线;当有5个点时,可作出10条直线,当有6点时,可作出15条直线.
②归纳:考察点的个数n和可作出直线的条数Sn发现如下表所示:Sn=$\frac{n(n-1)}{2}$.
③当有2006个点时,可作出直线的条数S2006=2011015.
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可作出3条直线;当有4个点时,可作出6条直线;当有5个点时,可作出10条直线,当有6点时,可作出15条直线.
②归纳:考察点的个数n和可作出直线的条数Sn发现如下表所示:Sn=$\frac{n(n-1)}{2}$.
| 点的个数 | 可连成直线条数 |
| 2 | l=S2=$\frac{2×1}{2}$ |
| 3 | 3=S3=$\frac{3×2}{2}$ |
| 4 | 6=S4=$\frac{4×3}{2}$ |
| 5 | 10=S5=$\frac{5×4}{2}$ |
| … | … |
| n | Sn=$\frac{n(n-1)}{2}$ |
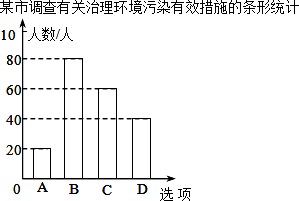 某市对市民进行了有关“治理环境污染”的问卷调查,调查问卷内容是“你认为下列哪种治理环境污染的措施最有效?”有以下四个选项(每份调查问卷必答且只选一个选项):
某市对市民进行了有关“治理环境污染”的问卷调查,调查问卷内容是“你认为下列哪种治理环境污染的措施最有效?”有以下四个选项(每份调查问卷必答且只选一个选项):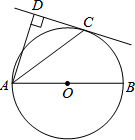 如图,AB是⊙O的直径,C是⊙O上一点,AD垂直与过点C的直线,垂足为D,AC平分∠BAD.
如图,AB是⊙O的直径,C是⊙O上一点,AD垂直与过点C的直线,垂足为D,AC平分∠BAD.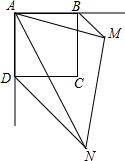 已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.
已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.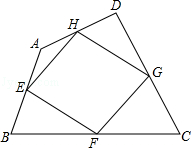 如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.
如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.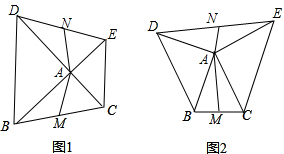
 如图所示,反比例函数y1=$\frac{6}{x}$的图象与一次函数y2=kx+b的图象交于点A(3,m),B(n,-3),一次函数图象与y轴交于点C.
如图所示,反比例函数y1=$\frac{6}{x}$的图象与一次函数y2=kx+b的图象交于点A(3,m),B(n,-3),一次函数图象与y轴交于点C.