题目内容
4.化简$\frac{16-{a}^{2}}{{a}^{2}+4a+4}$÷$\frac{a-4}{2a+4}•\frac{a+2}{a+4}$,其结果是-2.分析 原式先利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果.
解答 解:原式=$\frac{(4+a)(4-a)}{(a+2)^{2}}•\frac{2(a+2)}{a-4}•\frac{a+2}{a+4}$=-2,
故答案为:-2.
点评 此题考查了分式的乘除法,分式的乘除法运算的关键是约分,约分的关键是找公因式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.平面上有n个点(n≥2)且任意三个点不在同一直线上,过这些点中的任两点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可作出3条直线;当有4个点时,可作出6条直线;当有5个点时,可作出10条直线,当有6点时,可作出15条直线.
②归纳:考察点的个数n和可作出直线的条数Sn发现如下表所示:Sn=$\frac{n(n-1)}{2}$.
③当有2006个点时,可作出直线的条数S2006=2011015.
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可作出3条直线;当有4个点时,可作出6条直线;当有5个点时,可作出10条直线,当有6点时,可作出15条直线.
②归纳:考察点的个数n和可作出直线的条数Sn发现如下表所示:Sn=$\frac{n(n-1)}{2}$.
| 点的个数 | 可连成直线条数 |
| 2 | l=S2=$\frac{2×1}{2}$ |
| 3 | 3=S3=$\frac{3×2}{2}$ |
| 4 | 6=S4=$\frac{4×3}{2}$ |
| 5 | 10=S5=$\frac{5×4}{2}$ |
| … | … |
| n | Sn=$\frac{n(n-1)}{2}$ |
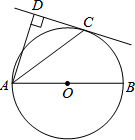 如图,AB是⊙O的直径,C是⊙O上一点,AD垂直与过点C的直线,垂足为D,AC平分∠BAD.
如图,AB是⊙O的直径,C是⊙O上一点,AD垂直与过点C的直线,垂足为D,AC平分∠BAD. 如图所示,反比例函数y1=$\frac{6}{x}$的图象与一次函数y2=kx+b的图象交于点A(3,m),B(n,-3),一次函数图象与y轴交于点C.
如图所示,反比例函数y1=$\frac{6}{x}$的图象与一次函数y2=kx+b的图象交于点A(3,m),B(n,-3),一次函数图象与y轴交于点C. 如图,在平行四边形ABCD中,∠FCD=∠EAB,∠BCE=∠DAF,求证:四边形FAEC是平行四边形.
如图,在平行四边形ABCD中,∠FCD=∠EAB,∠BCE=∠DAF,求证:四边形FAEC是平行四边形.