题目内容
如图，这是由一个边长为a的正方形沿一条对角线的方向平移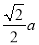
得到的图形，
① 数一数这个图案中共有几个正方形；
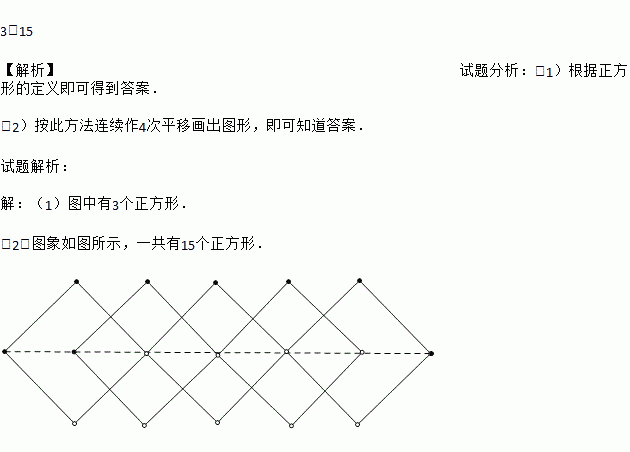
② 若按此方法连续做4次平移，可得怎样的图案？该图案中共有几个正方形？
3；15
【解析】试题分析：（1）根据正方形的定义即可得到答案．
（2）按此方法连续作4次平移画出图形，即可知道答案．
试题解析：
【解析】
（1）图中有3个正方形．
（2）图象如图所示，一共有15个正方形．
练习册系列答案
相关题目
请你用所学的知识，在下面两项中任选其一作图．
（1）参考下图，为班级的黑板报设计一组花边图案．
（2）以三角形、矩形、圆形为“基本图案”通过平移、旋转、轴对称为班级设计一个班徽．
见解析
【解析】试题分析：本题主要考查大家根据轴对称性质设计花边图案的能力，而且要符合考题中的四点要求，这是一道融数学与美术为一体的综合创新素质题
试题解析：【解析】
选（1）．如图：设计花边图案为： 计算：(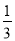
)-1－|－2＋
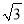tan45°|＋(
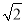－1.41)0＝________.
2＋
【解析】原式＝3－|－2＋|＋1＝4－2＋＝2＋，
故答案为：2+. －3x2＋2x－1＝____________＝－3x2＋_________.
－(3x2－2x＋1) (2x－1)
【解析】根据提公因式的要求，先提取负号，可得－(3x2－2x＋1)，再把2x-1看做一个整体去括号即可得（2x-1）.
故答案为：－(3x2－2x＋1) ，(2x－1). 把a2﹣4a多项式分解因式，结果正确的是（ ）
A. a（a﹣4） B. （a+2）（a﹣2） C. a（a+2）（a﹣2） D. （a﹣2）2﹣4
A
【解析】试题分析： a2-4a=a（a-4），
故选A． 如图所示，△EFG是由△ABC沿水平方向平移得到的，如果∠ABC＝90°，AB=3 cm，BC＝2 cm，则EF＝_________，FG=_________，EG＝_________．
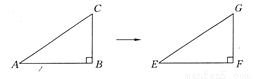
3 cm 2 cm cm
【解析】试题分析：在Rt△ABC中，AC＝＝＝（cm），
∵△EFG是由△ABC沿水平方向平移得到的，
∴EF＝AB＝3cm，FG＝BC＝2cm，EG＝AC＝cm．
故答案为3cm，2cm， cm． 在△ABC中，OE⊥AB，OF⊥AC且OE=OF．
（1）如图，当点O在BC边中点时，试说明AB=AC；
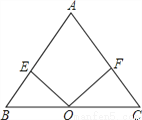
（2）如图，当点O在△ABC内部时，且OB=OC，试说明AB与AC的关系；
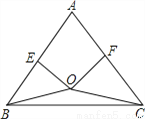
（3）当点O在△ABC外部时，且OB=OC，试判断AB与AC的关系．（画出图形，写出结果即可，无须说明理由）
见解析
【解析】试题分析：（1）证△BOE≌△COF，可得∠B=∠C，通过等角对等边，得出AB=AC；
（2）与（1）类似，在证得△BOE≌△COF后，得∠OBE=∠OCF，OB=OC；则∠OBC=∠OCB，可证得∠ABC=∠ACB，根据等角对等边得出AB=AC；
（3）由前两问的解答过程可知，BC的垂直平分线与∠A的角平分线重合时，AB=AC的结论才成立（等腰三角形三线合一）．... 如图所示，AB⊥BD，AC⊥CD，∠D=35°，则∠A的度数为（ ）
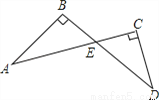
A. 65° B. 35° C. 55° D. 45°
B
【解析】【解析】
∵AB⊥BD，AC⊥CD，∴∠B=∠C=90°，∴∠A+∠AEB=∠D+∠CED=90°．
又∵∠AEB=∠CED，∴∠A=∠D=35°．故选B． 火车在笔直的铁路上开动，火车头以100千米/时的速度前进了半小时，则车尾走的路程是（ ）
A. 100千米 B. 50千米 C. 200千米 D. 无法计算
B
【解析】试题解析：在笔直的铁路上，火车头的速度和车尾的速度是相同的，所以在半个小时内车尾走的路程是50千米.
故选B.