题目内容
在△ABC中，高AD和BE交于H点，且BH=AC，则∠ABC=______．
45°或135°
【解析】【解析】
有2种情况．
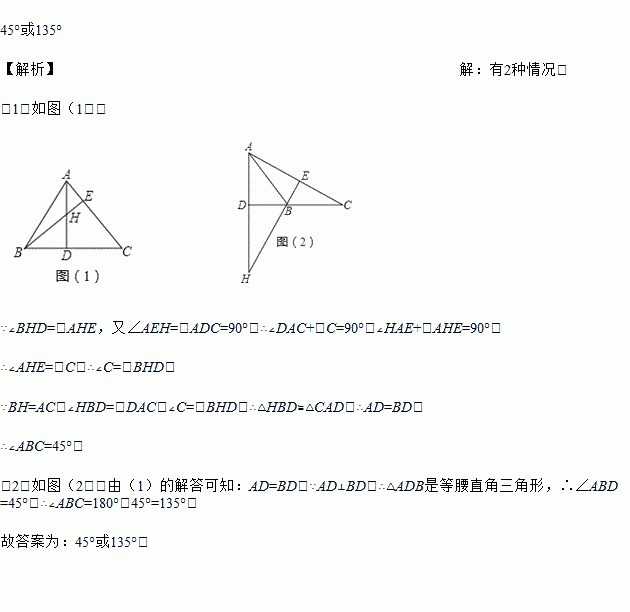
（1）如图（1）．
∵∠BHD=∠AHE，又∠AEH=∠ADC=90°，∴∠DAC+∠C=90°，∠HAE+∠AHE=90°，
∴∠AHE=∠C，∴∠C=∠BHD．
∵BH=AC，∠HBD=∠DAC，∠C=∠BHD，∴△HBD≌△CAD，∴AD=BD．
∴∠ABC=45°；
（2）如图（2）．由（1）的解...
练习册系列答案
相关题目
2cos30°的值等于
（A）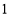
（B）
（C）
（D）
D．
【解析】
试题分析：根据特殊角的三角函数值直接解答即可．
试题解析：2cos30°=2×．
故选D． －3x2＋2x－1＝____________＝－3x2＋_________.
－(3x2－2x＋1) (2x－1)
【解析】根据提公因式的要求，先提取负号，可得－(3x2－2x＋1)，再把2x-1看做一个整体去括号即可得（2x-1）.
故答案为：－(3x2－2x＋1) ，(2x－1). 如图所示，△EFG是由△ABC沿水平方向平移得到的，如果∠ABC＝90°，AB=3 cm，BC＝2 cm，则EF＝_________，FG=_________，EG＝_________．
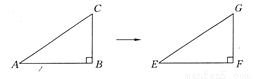
3 cm 2 cm cm
【解析】试题分析：在Rt△ABC中，AC＝＝＝（cm），
∵△EFG是由△ABC沿水平方向平移得到的，
∴EF＝AB＝3cm，FG＝BC＝2cm，EG＝AC＝cm．
故答案为3cm，2cm， cm． 在△ABC中，OE⊥AB，OF⊥AC且OE=OF．
（1）如图，当点O在BC边中点时，试说明AB=AC；
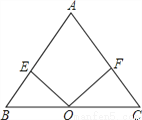
（2）如图，当点O在△ABC内部时，且OB=OC，试说明AB与AC的关系；
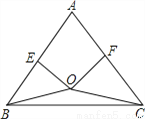
（3）当点O在△ABC外部时，且OB=OC，试判断AB与AC的关系．（画出图形，写出结果即可，无须说明理由）
见解析
【解析】试题分析：（1）证△BOE≌△COF，可得∠B=∠C，通过等角对等边，得出AB=AC；
（2）与（1）类似，在证得△BOE≌△COF后，得∠OBE=∠OCF，OB=OC；则∠OBC=∠OCB，可证得∠ABC=∠ACB，根据等角对等边得出AB=AC；
（3）由前两问的解答过程可知，BC的垂直平分线与∠A的角平分线重合时，AB=AC的结论才成立（等腰三角形三线合一）．... 下列说法错误的是（ ）
A. 直角三角板的两个锐角互余
B. 经过直线外一点只能画一条直线与已知直线平行
C. 如果两个角互补，那么，这两个角一定都是直角
D. 平行于同一条直线的两条直线平行
C
【解析】解：A．直角三角形中的两个锐角互余，所以直角三角板的两个锐角互余，故本选项说法正确；
B．根据平行公理可知：过直线外一点作已知直线的平行线，能作且只能作一条，故本选项说法正确；
C．如果两个角互补，那么，这两个角和一定是180°，但是它们不一定都是直角，故本选项说法错误；
D．根据平行线的传递性知平行于同一条直线的两条直线平行．故本选项说法正确．
故选C．... 如图所示，AB⊥BD，AC⊥CD，∠D=35°，则∠A的度数为（ ）
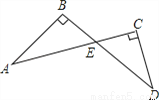
A. 65° B. 35° C. 55° D. 45°
B
【解析】【解析】
∵AB⊥BD，AC⊥CD，∴∠B=∠C=90°，∴∠A+∠AEB=∠D+∠CED=90°．
又∵∠AEB=∠CED，∴∠A=∠D=35°．故选B． 在等腰梯形ABCD中，∠ABC＝2∠ACB，BD平分∠ABC，AD∥BC，如图所示，则图中的等腰三角形有( )
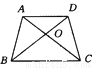
A. 1个 B. 2个 C. 3个 D. 4个
D
【解析】∵AD∥BC，∠ADB=30°，
∴∠CBD=∠ADB=30°.
∵ABCD为等腰梯形，
∴∠ABC=∠DCB=60°，则∠BAD=∠ABC-∠CBD=30°，
∴△ABD为等腰三角形.
同理可证△ACD为等腰三角形，
∵∠ABO=∠DCO=30°，∠AOB=∠DOC，AB=CD，
∴△AOB≌△DOC，
∴AO=DO，BO=CO，... 下列说法正确的是（ ）
A. x=1是不等式-2x＜1的解 B. x=3是不等式-x＜1的解集
C. x＞-2是不等式-2x＜1的解集 D. 不等式-x＜1的解集是x＜-1
A
【解析】试题分析：根据不等式的解集的定义及不等式的基本性质依次分析各项即可.
A.－2x＜1，，则x＝1是不等式－2x＜1的解集，本选项正确；
B.－x＜1，x＞－1，则x＝3是不等式－x＜1的解集，故本选项错误；
C.－2x＜1，，则x＞－2不是不等式－2x＜1的解集，故本选项错误；
D.不等式－x＜1的解集是x＞－1，故本选项错误；
故选A.