题目内容
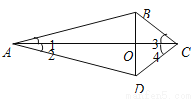
如图，四边形ABCD的对角线AC与BD相交于O点，∠1=∠2，∠3=∠4．
求证：(1)△ABC≌△ADC；(2)BO=DO．
(1)、证明过程见解析；(2)、证明过程见解析
【解析】试题分析：(1)、根据∠1=∠2，AC=AC，∠3=∠4得到△ABC和△ADC全等；(2)、根据全等得出AB=AD，然后结合∠1=∠2，AO=AO得出△ABO和△ADO全等，从而得到BO=DO.
试题解析：(1)、在△ABC和△ADC中∴△ABC≌△ADC．
(2)、∵△ABC≌△ADC ∴AB=AD 在△ABO和△ADO中...
练习册系列答案
互动英语系列答案
相关题目
计算：(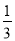
)-1－|－2＋
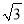tan45°|＋(
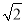－1.41)0＝________.
2＋
【解析】原式＝3－|－2＋|＋1＝4－2＋＝2＋，
故答案为：2+. 在△ABC中，OE⊥AB，OF⊥AC且OE=OF．
（1）如图，当点O在BC边中点时，试说明AB=AC；
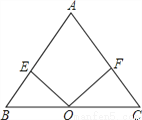
（2）如图，当点O在△ABC内部时，且OB=OC，试说明AB与AC的关系；
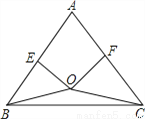
（3）当点O在△ABC外部时，且OB=OC，试判断AB与AC的关系．（画出图形，写出结果即可，无须说明理由）
见解析
【解析】试题分析：（1）证△BOE≌△COF，可得∠B=∠C，通过等角对等边，得出AB=AC；
（2）与（1）类似，在证得△BOE≌△COF后，得∠OBE=∠OCF，OB=OC；则∠OBC=∠OCB，可证得∠ABC=∠ACB，根据等角对等边得出AB=AC；
（3）由前两问的解答过程可知，BC的垂直平分线与∠A的角平分线重合时，AB=AC的结论才成立（等腰三角形三线合一）．... 如图所示，AB⊥BD，AC⊥CD，∠D=35°，则∠A的度数为（ ）
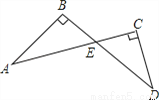
A. 65° B. 35° C. 55° D. 45°
B
【解析】【解析】
∵AB⊥BD，AC⊥CD，∴∠B=∠C=90°，∴∠A+∠AEB=∠D+∠CED=90°．
又∵∠AEB=∠CED，∴∠A=∠D=35°．故选B． 下列说法中不正确的是（ ）
A. 平行四边形是中心对称图形
B. 斜边及一锐角分别相等的两直角三角形全等
C. 两个锐角分别相等的两直角三角形全等
D. 一直角边及斜边分别相等的两直角三角形全等
C
【解析】解：A．平行四边形是中心对称图形，说法正确；
B．斜边及一锐角分别相等的两直角三角形全等，说法正确；
C．两个锐角分别相等的两直角三角形全等，说法错误；
D．一直角边及斜边分别相等的两直角三角形全等，说法正确．
故选C． 在等腰梯形ABCD中，∠ABC＝2∠ACB，BD平分∠ABC，AD∥BC，如图所示，则图中的等腰三角形有( )
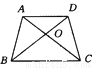
A. 1个 B. 2个 C. 3个 D. 4个
D
【解析】∵AD∥BC，∠ADB=30°，
∴∠CBD=∠ADB=30°.
∵ABCD为等腰梯形，
∴∠ABC=∠DCB=60°，则∠BAD=∠ABC-∠CBD=30°，
∴△ABD为等腰三角形.
同理可证△ACD为等腰三角形，
∵∠ABO=∠DCO=30°，∠AOB=∠DOC，AB=CD，
∴△AOB≌△DOC，
∴AO=DO，BO=CO，... 如果两个图形可以经过平移得到，那么这两个图形的面积 _____.
相等
【解析】试题解析：平移前后的两个图形是全等的，所以面积是相等的.
故答案为：相等. 火车在笔直的铁路上开动，火车头以100千米/时的速度前进了半小时，则车尾走的路程是（ ）
A. 100千米 B. 50千米 C. 200千米 D. 无法计算
B
【解析】试题解析：在笔直的铁路上，火车头的速度和车尾的速度是相同的，所以在半个小时内车尾走的路程是50千米.
故选B. 分解因式：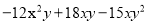 
【解析】试题分析：根据提公因式法--因式分解，确定公因式后提取公因式即可，注意公因式是相同字母，并且指数最小的.
试题解析：