题目内容
8. 如图,已知△ABC中,AB>AC,BD是AC边上中线,CE是AB边上中线,且BD⊥CE于点G,GF⊥BC于点F,若GF=2$\sqrt{2}$,BC=6,求AB的长.
如图,已知△ABC中,AB>AC,BD是AC边上中线,CE是AB边上中线,且BD⊥CE于点G,GF⊥BC于点F,若GF=2$\sqrt{2}$,BC=6,求AB的长.
分析 首先由射影定理求出BF,得出CF,再由射影定理求出BG2、CG,再根据重心定理求出EG,然后由勾股定理求出BE,即可得出AB的长.
解答 解:∵BD⊥CE,GF⊥BC,
∴由射影定理得:GF2=BF•CF=BF(BC-BF),
即(2$\sqrt{2}$)2=BF(6-BF),
解得:BF=4,或BF=2(不合题意,舍去),
∴BF=4,
∴CF=2,
由射影定理得:BG2=BF•BC=4×6=24,CG2=CF•BC=2×6=12,
∴CG=2$\sqrt{3}$,
∵BD是AC边上中线,CE是AB边上中线,
∴AB=2BE,
由重心定理得:EG=$\frac{1}{2}$CG=$\sqrt{3}$,
在Rt△BEG中,由勾股定理得:BE2=EG2+BG2=3+24=27,
∴BE=3$\sqrt{3}$,
∴AB=2BE=6$\sqrt{3}$.
点评 本题考查了勾股定理、射影定理、重心定理;熟练掌握勾股定理和重心定理,由射影定理和重心定理求出EG是解决问题的关键.

练习册系列答案
相关题目
16.方程ax+1=3的解是x=-2,则a的值是( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
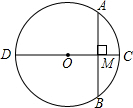 已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.
已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.
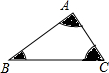 已知∠A+∠B+∠C=180°,分别以点A,B,C为顶点,1为直径画扇形,如图所示,阴影部分的面积为$\frac{π}{8}$.
已知∠A+∠B+∠C=180°,分别以点A,B,C为顶点,1为直径画扇形,如图所示,阴影部分的面积为$\frac{π}{8}$. 如图9个方格中,每行、每列、每条对角线上的三个数的和都相等.那么,右上角的数为2011.
如图9个方格中,每行、每列、每条对角线上的三个数的和都相等.那么,右上角的数为2011.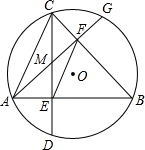 如图,在⊙O中,弦AB⊥弦CD于E,弦AG⊥弦BC于F点,CD与AG相交于M点.
如图,在⊙O中,弦AB⊥弦CD于E,弦AG⊥弦BC于F点,CD与AG相交于M点.