题目内容
13. 如图,△ABC内接⊙O中,AB=AC=5cm,BC=6cm,求⊙O的半径.
如图,△ABC内接⊙O中,AB=AC=5cm,BC=6cm,求⊙O的半径.
分析 连接OA,交BC于D,连接OB,根据垂径定理证得OA垂直平分BC,然后根据勾股定理即可求得AD,然后设半径为r,则OB=r,OD=r-4,根据勾股定理得出关于r的方程,解方程即可求得.
解答  解:连接OA,交BC于D,连接OB,
解:连接OA,交BC于D,连接OB,
∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴OA⊥BC,BD=CD,
∵BC=6cm,AB=AC=5cm,
∴BD=3cm,
在RT△ABD中,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4cm,
设半径为r,则OB=r,OD=r-4,
在RT△oBD中,r2=32+(r-4)2,
解得r=$\frac{25}{8}$.
点评 本题考查了垂径定理和勾股定理的应用,作出辅助线构建直角三角形是解题的关键.

练习册系列答案
相关题目
 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且AD⊥AB,求证:BC=AB+CD.
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且AD⊥AB,求证:BC=AB+CD.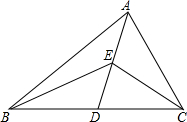 如图,在△ABC中,AD是中线,E是AD的中点,若△ABC的面积是24cm2,则△EBC的面积是12cm2.
如图,在△ABC中,AD是中线,E是AD的中点,若△ABC的面积是24cm2,则△EBC的面积是12cm2. 如图,在△ABC中,ED垂直平分AB,交AC于D,交AB于E,AC=5,BC=4.求△BCD的周长.
如图,在△ABC中,ED垂直平分AB,交AC于D,交AB于E,AC=5,BC=4.求△BCD的周长.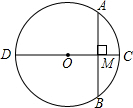 已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.
已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.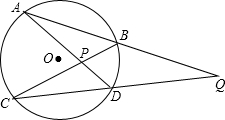 如图,⊙O的弦AB,CD的延长线相交于点Q,AD,CB相交于点P,试探索∠APC及∠Q的度数分别与$\widehat{AC}$和$\widehat{BD}$的度数有怎样的关系,并证明你的结论.
如图,⊙O的弦AB,CD的延长线相交于点Q,AD,CB相交于点P,试探索∠APC及∠Q的度数分别与$\widehat{AC}$和$\widehat{BD}$的度数有怎样的关系,并证明你的结论.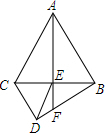 如图所示,△ACB,△ECD是等边三角形,且E点在BC上,AE的延长线交DB于F点,请你在图中找出一对全等三角形,并写出证明它们全等的过程.
如图所示,△ACB,△ECD是等边三角形,且E点在BC上,AE的延长线交DB于F点,请你在图中找出一对全等三角形,并写出证明它们全等的过程.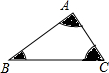 已知∠A+∠B+∠C=180°,分别以点A,B,C为顶点,1为直径画扇形,如图所示,阴影部分的面积为$\frac{π}{8}$.
已知∠A+∠B+∠C=180°,分别以点A,B,C为顶点,1为直径画扇形,如图所示,阴影部分的面积为$\frac{π}{8}$.