题目内容
9.已知点G是等边△ABC的重心,AB=6,P为AB边上的一个动点,则P、G两点间距离的最小值是( )| A. | 2 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
分析 根据点到直线之间垂线段最短可知,当GP⊥AB时GP最小,此时点P在线段AB的中点,根据重心的性质可得CG=2PG,即GP=$\frac{1}{3}$CP,只需运用勾股定理求出CP即可.
解答 解:当点P运动到AB中点位置时,
∵点G是等边△ABC的重心,
∴CP⊥AB,CG=2PG即GP=$\frac{1}{3}$CP.
此时GP最短,且BP=3,BC=6,
根据勾股定理可得:
CP=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴GP=$\sqrt{3}$.
故选C.
点评 本题主要考查了点到直线之间垂线段最短、重心的性质(即重心到顶点的距离等于重心到对应中点距离的2倍)、勾股定理等知识,运用重心的性质能提高解题速度,应熟练掌握.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
19.下列方程与方程2x2-x-2=0同解的是( )
| A. | (x-$\frac{1}{2}$)2=$\frac{5}{4}$ | B. | (x-$\frac{1}{2}$)2=$\frac{1}{4}$ | C. | (x-$\frac{1}{4}$)2=$\frac{9}{16}$ | D. | (x-$\frac{1}{4}$)2=$\frac{17}{16}$ |
 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且AD⊥AB,求证:BC=AB+CD.
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且AD⊥AB,求证:BC=AB+CD.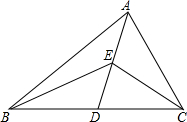 如图,在△ABC中,AD是中线,E是AD的中点,若△ABC的面积是24cm2,则△EBC的面积是12cm2.
如图,在△ABC中,AD是中线,E是AD的中点,若△ABC的面积是24cm2,则△EBC的面积是12cm2.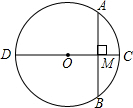 已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.
已知:如图,CD为⊙O的直径,AB为⊙O的弦.CD⊥AB,垂足为M,求证:AC=BC.