题目内容
2.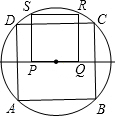 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )| A. | 1:2 | B. | 1:3 | C. | $\sqrt{2}$:3 | D. | 2:5 |
分析 设圆的半径为r,则OD=OR=r,DE=OE=$\frac{1}{2}$DC,OF=RS=2FR,由勾股定理得出OD2=r2=OE2+DE2=2DE2=$\frac{1}{2}$DC2,OR2=r2=OF2+FR2=$\frac{5}{4}$OF2,由正方形的面积公式即可得出结果.
解答 解:如图所示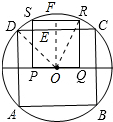 :
:
设圆半径为r,则OD=OR=r,DE=OE=$\frac{1}{2}$DC,OF=RS=2FR,
∴OD2=r2=OE2+DE2=2DE2=$\frac{1}{2}$DC2,
OR2=r2=OF2+FR2=$\frac{5}{4}$OF2,
∴S正方形ABCD=DC2=2r2,
S正方形PQRS=OF2=$\frac{4{r}^{2}}{5}$,
∴S正方形PQRS:S正方形ABCD=$\frac{\frac{4{r}^{2}}{5}}{2{r}^{2}}$=$\frac{2}{5}$.
故选:D.
点评 本题考查了正多边形和圆、正方形的性质、正方形面积的计算;熟练掌握正方形的性质是解决问题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
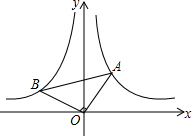 如图,点A是函数$y=\frac{a}{x}(a>0)$的图象在第一象限内分支上一点,过O点作OB⊥OA,交函数$y=-\frac{a}{x}(a>0)$的图象在第二象限内分支于点B.点C为x轴正半轴上一点.
如图,点A是函数$y=\frac{a}{x}(a>0)$的图象在第一象限内分支上一点,过O点作OB⊥OA,交函数$y=-\frac{a}{x}(a>0)$的图象在第二象限内分支于点B.点C为x轴正半轴上一点.
 如图,一铁路路基的横断面是等腰梯形ABCD,AD=BC,CD=8m,路基的高度DE=6m,斜坡BC的坡比是1:$\sqrt{3}$,求路基下底宽AB的长度.
如图,一铁路路基的横断面是等腰梯形ABCD,AD=BC,CD=8m,路基的高度DE=6m,斜坡BC的坡比是1:$\sqrt{3}$,求路基下底宽AB的长度. 如图,已知⊙O中,过圆内一点E作⊙O的两条弦AB和CD,AE=DE,求证:$\widehat{AC}=\widehat{BD}$.
如图,已知⊙O中,过圆内一点E作⊙O的两条弦AB和CD,AE=DE,求证:$\widehat{AC}=\widehat{BD}$. 如图,△ABC中,CD是高,BC+BD=AD,求证:∠ABC=2∠A.
如图,△ABC中,CD是高,BC+BD=AD,求证:∠ABC=2∠A.