题目内容
10.解方程:$\frac{x}{{x}^{2}-4}$+$\frac{2}{x+2}$=$\frac{1}{x-2}$.分析 利用解分式方程的步骤与方法求得方程的解即可.
解答 解:$\frac{x}{{x}^{2}-4}$+$\frac{2}{x+2}$=$\frac{1}{x-2}$
方程两边同乘(x+2)(x-2)得
x+2(x-2)=x+2
解得:x=3
检验:当x=3,(x+2)(x-2)≠0,
所以原分式方程的解为x=3.
点评 此题考查解分式方程,掌握解分式方程的步骤与方法是解决问题的关键.

练习册系列答案
相关题目
2.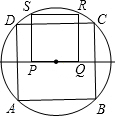 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )| A. | 1:2 | B. | 1:3 | C. | $\sqrt{2}$:3 | D. | 2:5 |
20.用边长为4cm,5cm,6cm的两个全等三角形拼成四边形,一共能拼成( )个平行四边形.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
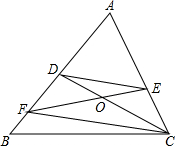 如图,在△ABC中,∠ACD=∠B,将△ACD绕A点旋转,点D落在点E处,点C落在点F处,CD,EF交于O点,连接DE,FC,找出其中相似三角形.
如图,在△ABC中,∠ACD=∠B,将△ACD绕A点旋转,点D落在点E处,点C落在点F处,CD,EF交于O点,连接DE,FC,找出其中相似三角形.
