题目内容
14. 如图,一铁路路基的横断面是等腰梯形ABCD,AD=BC,CD=8m,路基的高度DE=6m,斜坡BC的坡比是1:$\sqrt{3}$,求路基下底宽AB的长度.
如图,一铁路路基的横断面是等腰梯形ABCD,AD=BC,CD=8m,路基的高度DE=6m,斜坡BC的坡比是1:$\sqrt{3}$,求路基下底宽AB的长度.
分析 分别过D、C作梯形的高DE、CF,则DE=CF=6m,EF=DC=8m,由斜坡BC的坡比是1:$\sqrt{3}$,根据坡比的概念得到CF:BF=1:$\sqrt{3}$,可计算出BF,再根据等腰梯形的性质得AE=BF=6$\sqrt{3}$m,利用AB=AE+EF+BF计算即可.
解答  解:分别过D、C作梯形的高DE、CF,如图
解:分别过D、C作梯形的高DE、CF,如图
∴DE=CF=6m,EF=DC=8m,
∵斜坡BC的坡比是1:$\sqrt{3}$,
∴CF:BF=1:$\sqrt{3}$,
∴BF=$\sqrt{3}$CF=6$\sqrt{3}$m,
又∵四边形为等腰梯形,
∴AE=BF=6$\sqrt{3}$m,
∴AB=6$\sqrt{3}$m+8m+6$\sqrt{3}$m=(12$\sqrt{3}$+8)m.
故路基下底宽AB的长度为(12$\sqrt{3}$+8)m.
点评 本题考查了解直角三角形的应用-坡度坡角问题,等腰梯形的性质.掌握坡比的概念是解题的关键,坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
2.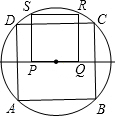 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )| A. | 1:2 | B. | 1:3 | C. | $\sqrt{2}$:3 | D. | 2:5 |



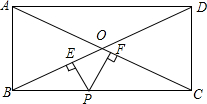 矩形ABCD中,AB=6,BC=8,P是BC边上的一点,PE⊥BD,PF⊥AC,垂足分别为E,F.求证:PE+PF为定值.
矩形ABCD中,AB=6,BC=8,P是BC边上的一点,PE⊥BD,PF⊥AC,垂足分别为E,F.求证:PE+PF为定值. 如图所示,半径为1的圆盘O竖直放在水平的地面上,圆盘外绕有细线(没有弹性),假设细线的末端最初在距地面高度为1米的点P处,现紧拉线的末端让它渐渐离开圆盘至点Q处,此时细线段TQ对应的直线与圆盘相切于点T.若TQ=$\frac{π}{3}$米,则Q点距离地面的高度为$\frac{3\sqrt{3}-π+6}{6}$米.
如图所示,半径为1的圆盘O竖直放在水平的地面上,圆盘外绕有细线(没有弹性),假设细线的末端最初在距地面高度为1米的点P处,现紧拉线的末端让它渐渐离开圆盘至点Q处,此时细线段TQ对应的直线与圆盘相切于点T.若TQ=$\frac{π}{3}$米,则Q点距离地面的高度为$\frac{3\sqrt{3}-π+6}{6}$米.