题目内容
12. 如图,△ABC中,CD是高,BC+BD=AD,求证:∠ABC=2∠A.
如图,△ABC中,CD是高,BC+BD=AD,求证:∠ABC=2∠A.
分析 在AD上取点E,使AE=CB,则DE=BD,可证得CB=CE,再利用等腰三角形的性质和外角的性质可得到结论.
解答 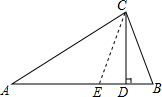 证明:在AD上取点E,使AE=CB,
证明:在AD上取点E,使AE=CB,
∵BC+BD=AD,
∴DE=BD,
∵CD是BA边上的高,
∴CD是BE的垂直平分线,
∴CB=CE=AE
∴∠B=∠CEB=2∠A.
点评 本题主要考查等腰三角形的性质和判定,与线段的和差有关的问题,一般是把几条线段转化在一条直线来解决.

练习册系列答案
相关题目
2.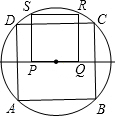 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )
如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( )| A. | 1:2 | B. | 1:3 | C. | $\sqrt{2}$:3 | D. | 2:5 |
20.用边长为4cm,5cm,6cm的两个全等三角形拼成四边形,一共能拼成( )个平行四边形.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
7.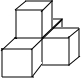 如图是由五个大小相同的小立方块搭成的几何体,下列说法正确的是( )
如图是由五个大小相同的小立方块搭成的几何体,下列说法正确的是( )
 如图是由五个大小相同的小立方块搭成的几何体,下列说法正确的是( )
如图是由五个大小相同的小立方块搭成的几何体,下列说法正确的是( )| A. | 从正面看到的形状图面积最小 | B. | 从左面看到的形状图面积最小 | ||
| C. | 从上面看到的形状图面积最小 | D. | 三个方向看到的形状图面积一样大 |
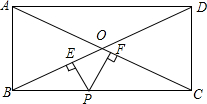 矩形ABCD中,AB=6,BC=8,P是BC边上的一点,PE⊥BD,PF⊥AC,垂足分别为E,F.求证:PE+PF为定值.
矩形ABCD中,AB=6,BC=8,P是BC边上的一点,PE⊥BD,PF⊥AC,垂足分别为E,F.求证:PE+PF为定值. 如图所示,已知等边三角形ABC的外接圆⊙O的半径为R,求△ABC的边长a、周长P、边心距r及面积S.
如图所示,已知等边三角形ABC的外接圆⊙O的半径为R,求△ABC的边长a、周长P、边心距r及面积S. 如图所示,半径为1的圆盘O竖直放在水平的地面上,圆盘外绕有细线(没有弹性),假设细线的末端最初在距地面高度为1米的点P处,现紧拉线的末端让它渐渐离开圆盘至点Q处,此时细线段TQ对应的直线与圆盘相切于点T.若TQ=$\frac{π}{3}$米,则Q点距离地面的高度为$\frac{3\sqrt{3}-π+6}{6}$米.
如图所示,半径为1的圆盘O竖直放在水平的地面上,圆盘外绕有细线(没有弹性),假设细线的末端最初在距地面高度为1米的点P处,现紧拉线的末端让它渐渐离开圆盘至点Q处,此时细线段TQ对应的直线与圆盘相切于点T.若TQ=$\frac{π}{3}$米,则Q点距离地面的高度为$\frac{3\sqrt{3}-π+6}{6}$米.