题目内容
13．点M（m+1，m+3）在x轴上，则点M坐标为（-2，0）．分析 根据x轴上点的纵坐标为0列方程求出m的值，再求解即可．
解答 解：∵点M（m+1，m+3）在x轴上，
∴m+3=0，
解得m=-3，
m+1=-3+1=-2，
所以，点M的坐标为（-2，0）．
故答案为：（-2，0）．
点评 本题考查了点的坐标，熟记x轴上点的纵坐标为0是解题的关键．
练习册系列答案
相关题目
16．
如图，直线a∥b，直线c分别与直线a，b相交于点A，B，且AC垂直直线c于点A，若∠1=40°，则∠2的度数为（ ）
如图，直线a∥b，直线c分别与直线a，b相交于点A，B，且AC垂直直线c于点A，若∠1=40°，则∠2的度数为（ ）| A． | 140° | B． | 90° | C． | 50° | D． | 40° |
4．
如图，在△ABC中，D为AB的中点，CE=3BE，CF=2AF，四边形CEDF的面积为17，则△ABC的面积为（ ）
如图，在△ABC中，D为AB的中点，CE=3BE，CF=2AF，四边形CEDF的面积为17，则△ABC的面积为（ ）| A． | 22 | B． | 23 | C． | 24 | D． | 25 |
1．
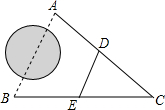如图，A、B两地被建筑物阻隔，为测量A、B两地间的距离，在地面上选一点C，连接CA、CB，分别取CA、CB的中点D、E，若测得DE的长为36m，那么A、B两地间的距离是（ ）
如图，A、B两地被建筑物阻隔，为测量A、B两地间的距离，在地面上选一点C，连接CA、CB，分别取CA、CB的中点D、E，若测得DE的长为36m，那么A、B两地间的距离是（ ）| A． | 60m | B． | 65m | C． | 70m | D． | 72m |
8．
如图，AB⊥CD于D，DE⊥DF，若∠BDE=60°，则∠CDF等于（ ）
如图，AB⊥CD于D，DE⊥DF，若∠BDE=60°，则∠CDF等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 120° |
5．下列式子中正确的是（ ）
| A． | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | B． | $\sqrt{{a^2}-{b^2}}$=a-b | C． | $\frac{\sqrt{6}+\sqrt{8}}{2}$=$\sqrt{3}$+$\sqrt{4}$=$\sqrt{3}$+2 | D． | a$\sqrt{x}$-b$\sqrt{x}$=（a-b）$\sqrt{x}$ |
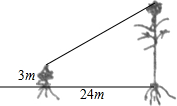有一只喜鹊在一棵3m高的小树上觅食，它的巢筑在距离该树24m远的一棵大树上，大树高14m，且巢离树顶部1m，当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5m/s，那它至少需要多少时间才能赶回巢中？（画出符合题意的几何图形，并求解）