题目内容
1.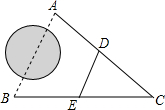 如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E,若测得DE的长为36m,那么A、B两地间的距离是( )
如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E,若测得DE的长为36m,那么A、B两地间的距离是( )| A. | 60m | B. | 65m | C. | 70m | D. | 72m |
分析 根据三角形中位线定理可知DE=$\frac{1}{2}$AB,由此即可解决问题.
解答 解: ∵AD=DC,BE=EC,
∵AD=DC,BE=EC,
∴DE∥AB,DE=$\frac{1}{2}$AB,
∵DE=36m,
∴AB=72m.
故选D.
点评 本题考查三角形中位线性质,解题的关键是灵活应用三角形中位定理识解决问题,属于中考常考题型.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
16.顺次连接矩形四边中点得到的四边形一定是( )
| A. | 矩形 | B. | 菱形 | C. | 等腰梯形 | D. | 正方形 |
6.已知点A(0,-4),B(8,0)和C(a,-a),若过点C的圆的圆心是线段AB的中点,则这个圆的半径的最小值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
11.因式分解的结果是(x+y-z)(x-y+z)的多项式是( )
| A. | x2-(y+z)2 | B. | (x-y)2-z2 | C. | -(x-y)2+z2 | D. | x2-(y-z)2 |
 如图,在梯形ABCD中,AD∥BC,AD=1,BC=4,AC=3,BD=4,则梯形ABCD的面积为6.
如图,在梯形ABCD中,AD∥BC,AD=1,BC=4,AC=3,BD=4,则梯形ABCD的面积为6.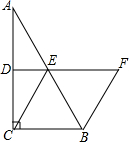 如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.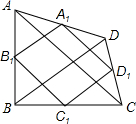 如图,四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm,点A1,B1,C1,D1是四边形ABCD各边上的中点,则四边形A1B1C1D1的周长为9cm.
如图,四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm,点A1,B1,C1,D1是四边形ABCD各边上的中点,则四边形A1B1C1D1的周长为9cm. 如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.