题目内容
3．
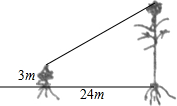有一只喜鹊在一棵3m高的小树上觅食，它的巢筑在距离该树24m远的一棵大树上，大树高14m，且巢离树顶部1m，当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5m/s，那它至少需要多少时间才能赶回巢中？（画出符合题意的几何图形，并求解）
分析 根据题意，构建直角三角形，利用勾股定理解答．
解答 
解：如图，由题意知AB=3m，CD=14-1=13（m），BD=24m．
过A作AE⊥CD于E．则CE=13-3=10（m），AE=24m，
在Rt△AEC中，
AC2=CE2+AE2=102+242．
故AC=26m，
则26÷5=5.2（s），
答：它至少需要5.2s才能赶回巢中．
点评 本题考查了勾股定理的应用，善于观察题目的信息是解题以及学好数学的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．
如图，△ABC中，边BC=12，高AD=6．矩形MNPQ的边在BC上，顶点P在AB上，顶点N在AC上，若S矩形MNPQ=y，PN=x，则y与x的关系式为（ ）
如图，△ABC中，边BC=12，高AD=6．矩形MNPQ的边在BC上，顶点P在AB上，顶点N在AC上，若S矩形MNPQ=y，PN=x，则y与x的关系式为（ ）| A． | y=6-$\frac{1}{2}$x（0＜x＜12） | B． | y=-$\frac{1}{2}$x2+6x（0＜x＜12） | ||
| C． | y=2x2-12x（0＜x＜12） | D． | y=$\frac{1}{2}$x2+6x（0＜x＜12） |
11．因式分解的结果是（x+y-z）（x-y+z）的多项式是（ ）
| A． | x2-（y+z）2 | B． | （x-y）2-z2 | C． | -（x-y）2+z2 | D． | x2-（y-z）2 |
8．
在平面直角坐标系中，正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置，其中点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3…在x轴上．已知正方形A1B1C1D1的边长为1，∠C1B1O=30°，B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是（ ）
在平面直角坐标系中，正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置，其中点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3…在x轴上．已知正方形A1B1C1D1的边长为1，∠C1B1O=30°，B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是（ ）| A． | ${（\frac{1}{2}）}^{2015}$ | B． | ${（\frac{1}{2}）}^{2016}$ | C． | ${（\frac{\sqrt{3}}{3}）}^{2015}$ | D． | ${（\frac{\sqrt{3}}{3}）}^{2016}$ |
15．
如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE与BF相交于O；下列结论：
（1）AE=BF；（2）AE⊥BF；（3）AD=OE；（4）S△AOB=S四边形DEOF．
其中正确的有（ ）
如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE与BF相交于O；下列结论：（1）AE=BF；（2）AE⊥BF；（3）AD=OE；（4）S△AOB=S四边形DEOF．
其中正确的有（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
12．
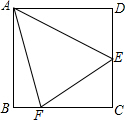如图，在边长为$6\sqrt{2}$的正方形ABCD中，E是边CD的中点，F在BC边上，且∠EAF=45°，连接EF，则BF的长为（ ）
如图，在边长为$6\sqrt{2}$的正方形ABCD中，E是边CD的中点，F在BC边上，且∠EAF=45°，连接EF，则BF的长为（ ）| A． | $2\sqrt{2}$ | B． | 3 | C． | $3\sqrt{2}$ | D． | 4 |
