题目内容
19.观察下面三个特殊的等式1×2=$\frac{1}{3}$(1×2×3-0×1×2)
2×3=$\frac{1}{3}$(2×3×4-1×2×3)
3×4=$\frac{1}{3}$(3×4×5-1×2×3×4)
将这三个等式的两边相加,可以得到1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20
读完这段材料,请你思考后回答:
(1)1×2+2×3+…+100×101=343400;
(2)1×2+2×3+3×4+…+n×(n+1)=$\frac{1}{3}$n(n+1)(n+2)..
(只需写出结果,不必写中间的过程)
分析 根据1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20可以得出,连续两个自然数的乘积的和等于后面一个算式的两个数字再与最后一个数字加1相乘积的$\frac{1}{3}$,由此得出一般性规律1×2+2×3+…+n(n+1)=$\frac{1}{3}$n(n+1)(n+2)解决问题.
解答 解:(1)1×2+2×3+…+100×101=343400;
(2)1×2+2×3+3×4+…+n×(n+1)=$\frac{1}{3}$n(n+1)( n+2).
(1)$\frac{1}{3}$×100×101×102=343400;
故答案为:(2)$\frac{1}{3}$n(n+1)( n+2).
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律,利用规律解决问题.

练习册系列答案
相关题目
7.已知两圆的半径分别为1和4,圆心距为4,则两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
8.已知B、C两点把线段AD分成2:3:4三部分,M是AD的中点,CD=12,则MC的长为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
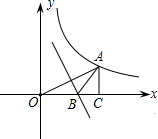 如图,已知点A在双曲线y=$\frac{6}{x}$上,且OA=4,过A作AC⊥x轴于C,OA的垂直平分线交OC于B,则△AOC的面积为3.
如图,已知点A在双曲线y=$\frac{6}{x}$上,且OA=4,过A作AC⊥x轴于C,OA的垂直平分线交OC于B,则△AOC的面积为3.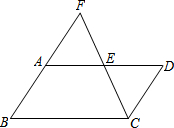 已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.猜想AB与AF有什么关系?为什么?
已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.猜想AB与AF有什么关系?为什么?