题目内容
8.已知B、C两点把线段AD分成2:3:4三部分,M是AD的中点,CD=12,则MC的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
分析 根据比例,可得AB、BC的长,根据线段的和差,可得AD的长,根据线段中点的性质,可得AM的长,根据线段的和差,可得答案.
解答 解:如图: ,
,
AB:BC:CD=2:3:4,CD=12,
∴AB=6,BC=9.
∴AD=AB+BC+CD=6+9+12=27,
M是AD的中点,
AM=$\frac{1}{2}$AD=$\frac{27}{2}$,
由线段的和差得AC=AB+BC=6+9=15,
MC=AC-AM=15-$\frac{27}{2}$=$\frac{3}{2}$.
故选C.
点评 本题考查了两点间的距离.利用了线段的和差,线段中点的性质.

练习册系列答案
相关题目
16.某位射击运动员在同一条件下进行射击,结果如下表:
(1)计算并填写表格中击中靶心的频率;
(2)该运动员射击一次,击中靶心的概率近似值是多少?并说明理由.
| 射击次数(n) | 8 | 15 | 20 | 30 | 40 | 50 |
| 击中靶心频数(m) | 6 | 12 | 17 | 24 | 32 | 40 |
| 击中靶心频率($\frac{m}{n}$) | 0.75 | 0.80 | 0.85 | 0.80 | 0.80 | 0.80 |
(2)该运动员射击一次,击中靶心的概率近似值是多少?并说明理由.
3.下列关于一元二次方程的根判断,说法一定正确的是( )
| A. | 方程x2-x+1=0的两实数根之和等于-1 | |
| B. | 方程x2+x+1=0的两实数根之积等于1 | |
| C. | 方程x2-x-1=0的两实数根之和等于1 | |
| D. | 方程x2+x-1=0的两实数根之积等于1 |
17.已知a、b是有理数,且a>b,则下列式子不正确的是( )
| A. | a+2>b+2 | B. | a-2>b-2 | C. | 2a>2b | D. | -2a>-2b |
18.若分式1-$\frac{3}{x+2}$的值为0,则x的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |


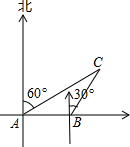 如图所示,某船以每小时40海里的速度向正东方向航行,在点A测得岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛C在北偏东30方向上,已知该岛周围18海里内有暗礁.
如图所示,某船以每小时40海里的速度向正东方向航行,在点A测得岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛C在北偏东30方向上,已知该岛周围18海里内有暗礁.