题目内容
14.若规定一种运算为:a★b=$\sqrt{2}$(b-a),如3★5=$\sqrt{2}$(5-3)=2$\sqrt{2}$.则$\sqrt{6}$★$\sqrt{3}$=$\sqrt{6}$-2$\sqrt{3}$.分析 先根据新定义得到$\sqrt{6}$★$\sqrt{3}$=$\sqrt{2}$($\sqrt{3}$-$\sqrt{6}$),然后进行二次根式的乘法运算即可.
解答 解:$\sqrt{6}$★$\sqrt{3}$=$\sqrt{2}$($\sqrt{3}$-$\sqrt{6}$)=$\sqrt{6}$-2$\sqrt{3}$.
故答案为$\sqrt{6}$-2$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了新定义.

练习册系列答案
相关题目
9.其中,从左面看到的形状图是平行四边形的有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
6.不等式组$\left\{\begin{array}{l}x+2<3\\-2x<4\end{array}$的解集是( )
| A. | -2<x<1 | B. | x<1 | C. | x>-2 | D. | x<-2 |
3.下列关于一元二次方程的根判断,说法一定正确的是( )
| A. | 方程x2-x+1=0的两实数根之和等于-1 | |
| B. | 方程x2+x+1=0的两实数根之积等于1 | |
| C. | 方程x2-x-1=0的两实数根之和等于1 | |
| D. | 方程x2+x-1=0的两实数根之积等于1 |
 已知如图,∠BAC=90°,AD⊥BC,∠1=∠2,EF⊥BC,求证:$\frac{EF}{DF}=\frac{BC}{AC}$.
已知如图,∠BAC=90°,AD⊥BC,∠1=∠2,EF⊥BC,求证:$\frac{EF}{DF}=\frac{BC}{AC}$.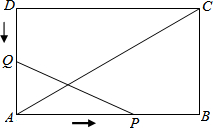 如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t(s)表示运动时间(0≤t≤6).
如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t(s)表示运动时间(0≤t≤6).