题目内容
7.已知两圆的半径分别为1和4,圆心距为4,则两圆的位置关系是( )| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
分析 先求两圆半径的和与差,再与圆心距进行比较,确定两圆的位置关系.
解答 解:因为圆心距=4,两圆半径差=4-1=3<4,两圆半径和=4+1=5>4,
根据圆心距与半径之间的数量关系可知,两圆的位置关系是内相交.
故选:C.
点评 本题考查了由数量关系来判断两圆位置关系的方法.设两圆的半径分别为R和r,且R≥r,圆心距为d:外离d>R+r;外切d=R+r;相交R-r<d<R+r;内切d=R-r;内含d<R-r.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.某位射击运动员在同一条件下进行射击,结果如下表:
(1)计算并填写表格中击中靶心的频率;
(2)该运动员射击一次,击中靶心的概率近似值是多少?并说明理由.
| 射击次数(n) | 8 | 15 | 20 | 30 | 40 | 50 |
| 击中靶心频数(m) | 6 | 12 | 17 | 24 | 32 | 40 |
| 击中靶心频率($\frac{m}{n}$) | 0.75 | 0.80 | 0.85 | 0.80 | 0.80 | 0.80 |
(2)该运动员射击一次,击中靶心的概率近似值是多少?并说明理由.
17.已知a、b是有理数,且a>b,则下列式子不正确的是( )
| A. | a+2>b+2 | B. | a-2>b-2 | C. | 2a>2b | D. | -2a>-2b |
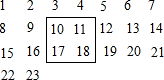 把正整数1,2,3,4,5,6,7…按如图方式排列成一个“数阵”.
把正整数1,2,3,4,5,6,7…按如图方式排列成一个“数阵”.
 如图,一个高8cm圆锥形零件,底面圆直径12cm,此圆锥的侧面积是60πcm2(结果保留π).
如图,一个高8cm圆锥形零件,底面圆直径12cm,此圆锥的侧面积是60πcm2(结果保留π). 已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).