题目内容
11.某课题小组为了了解某品牌电动自行车的销售情况,对某专卖店第一季度该品牌A、B、C、D四种型号的销售做了统计,绘制成如下两幅统计图(均不完整).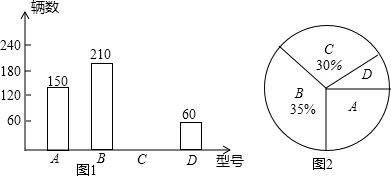
(1)该店第一季度售出这种品牌的电动自行车共多少辆?
(2)求出第一季度C型号的销售量和A、D两型号销售量所占的百分比,并把两幅统计图补充完整;
(3)若该专卖店计划订购这四款型号的电动自行车1800辆,求C型号电动自行车应订购多少辆?
分析 (1)根据B品牌210辆占总体的35%,即可求得总体;
(2)根据(1)中求得的总数和扇形统计图中C品牌所占的百分比即可求得C品牌的数量,进而补全条形统计图;根据条形统计图中A、D的数量和总数即可求得所占的百分比,从而补全扇形统计图;
(3)根据扇形统计图所占的百分比即可求解.
解答 解:(1)210÷35%=600(辆)
答:该店第一季度售出这种品牌的电动自行车共600辆.
(2)C品牌:600×30%=180;
A品牌:150÷600=25%;
D品牌:60÷600=10%.
(3)1800×30%=540(辆).
答:C型电动自行车应订购540辆.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.

练习册系列答案
相关题目
6.不等式组$\left\{\begin{array}{l}x+2<3\\-2x<4\end{array}$的解集是( )
| A. | -2<x<1 | B. | x<1 | C. | x>-2 | D. | x<-2 |
16.某位射击运动员在同一条件下进行射击,结果如下表:
(1)计算并填写表格中击中靶心的频率;
(2)该运动员射击一次,击中靶心的概率近似值是多少?并说明理由.
| 射击次数(n) | 8 | 15 | 20 | 30 | 40 | 50 |
| 击中靶心频数(m) | 6 | 12 | 17 | 24 | 32 | 40 |
| 击中靶心频率($\frac{m}{n}$) | 0.75 | 0.80 | 0.85 | 0.80 | 0.80 | 0.80 |
(2)该运动员射击一次,击中靶心的概率近似值是多少?并说明理由.
3.下列关于一元二次方程的根判断,说法一定正确的是( )
| A. | 方程x2-x+1=0的两实数根之和等于-1 | |
| B. | 方程x2+x+1=0的两实数根之积等于1 | |
| C. | 方程x2-x-1=0的两实数根之和等于1 | |
| D. | 方程x2+x-1=0的两实数根之积等于1 |
 在如图的正方形网格中,按照以下要求作图(不用写作图方法):
在如图的正方形网格中,按照以下要求作图(不用写作图方法):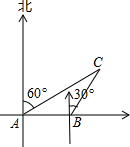 如图所示,某船以每小时40海里的速度向正东方向航行,在点A测得岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛C在北偏东30方向上,已知该岛周围18海里内有暗礁.
如图所示,某船以每小时40海里的速度向正东方向航行,在点A测得岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛C在北偏东30方向上,已知该岛周围18海里内有暗礁.