题目内容
4.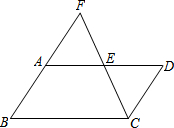 已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.猜想AB与AF有什么关系?为什么?
已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.猜想AB与AF有什么关系?为什么?
分析 由?ABCD中,点E是AD的中点,易证得△AEF≌△DEC,继而证得AF=CD,又由AB=CD,即可证得AB=AF.
解答 解:AB=AF.
理由:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠F=∠ECD,
∵点E是AD的中点,
即AE=DE,
在△AEF和△DEC中,
$\left\{\begin{array}{l}{∠F=∠ECD}\\{∠AEF=∠DEC}\\{AE=DE}\end{array}\right.$,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∴AB=AF.
点评 此题考查了平行四边形的性质以及全等三角形的判定与性质.注意证得△AEF≌△DEC是关键.

练习册系列答案
相关题目
16.某位射击运动员在同一条件下进行射击,结果如下表:
(1)计算并填写表格中击中靶心的频率;
(2)该运动员射击一次,击中靶心的概率近似值是多少?并说明理由.
| 射击次数(n) | 8 | 15 | 20 | 30 | 40 | 50 |
| 击中靶心频数(m) | 6 | 12 | 17 | 24 | 32 | 40 |
| 击中靶心频率($\frac{m}{n}$) | 0.75 | 0.80 | 0.85 | 0.80 | 0.80 | 0.80 |
(2)该运动员射击一次,击中靶心的概率近似值是多少?并说明理由.

 如图,一个高8cm圆锥形零件,底面圆直径12cm,此圆锥的侧面积是60πcm2(结果保留π).
如图,一个高8cm圆锥形零件,底面圆直径12cm,此圆锥的侧面积是60πcm2(结果保留π). 已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).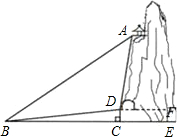 某景区有一个景观奇异的天门洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处,在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.
某景区有一个景观奇异的天门洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处,在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.