题目内容
6．下列运算中，正确的是（ ）| A． | 2a-a=1 | B． | a+a=2a | C． | （a3）3=a6 | D． | a8÷a2=a4 |
分析 分别利用合并同类项法则以及结合幂的乘方运算法则以及同底数幂的除法运算法则化简求出答案．
解答 解：A、2a-a=a，故此选项错误；
B、a+a=2a，故此选项正确；
C、（a3）3=a9，故此选项错误；
D、a8÷a2=a6，故此选项错误．
故选：B．
点评 此题主要考查了合并同类项以及幂的乘方运算、同底数幂的除法运算等知识，正确掌握相关运算法则是解题关键．
练习册系列答案
相关题目
16．
图示为一张直角三角形的纸片，两直角边AC=4cm，BC=8cm，现将△ABC沿DE折叠，使点B与点A重合，则CD的长为（ ）
图示为一张直角三角形的纸片，两直角边AC=4cm，BC=8cm，现将△ABC沿DE折叠，使点B与点A重合，则CD的长为（ ）| A． | 3cm | B． | 4cm | C． | 5cm | D． | 6cm |
17．
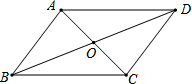如图，?ABCD中，对角线AC、BD相交于点O，下列说法一定正确的是（ ）
如图，?ABCD中，对角线AC、BD相交于点O，下列说法一定正确的是（ ）| A． | AO=BO | B． | AC⊥BD | C． | AB=BC | D． | AB=CD |
14．计算：（2ab2）3-（9ab2）（-ab2）2，结果正确的是（ ）
| A． | 17a3b6 | B． | 8a6b12 | C． | -a3b6 | D． | 15a3b6 |
1．将一元二次方程x2+2$\sqrt{2}$x+1=0左边配方成完全平方式之后，右边的常数应该是（ ）
| A． | 2 | B． | 1 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
二次函数y=ax2+bx+c的图象如图所示，下列结论：①a+c＞b；②4ac＜b2；③2a+b＞0．其中正确的有（ ）
18．
如图，点A、B、C、D在⊙O上，DE⊥OA，DF⊥OB，垂足分别为E，F，若∠EDF=50°，则∠C的度数为（ ）
如图，点A、B、C、D在⊙O上，DE⊥OA，DF⊥OB，垂足分别为E，F，若∠EDF=50°，则∠C的度数为（ ）| A． | 40° | B． | 50° | C． | 65° | D． | 130° |
15．
如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为$（\sqrt{2}，\sqrt{2}）$，点C的坐标为（1，0），点P为斜边OB上的一动点，则PA+PC的最小值为（ ）
如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为$（\sqrt{2}，\sqrt{2}）$，点C的坐标为（1，0），点P为斜边OB上的一动点，则PA+PC的最小值为（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\frac{{\sqrt{3}}}{2}$ |
16．
如图，延长正方形ABCD的边CB到E，使BE=AC，则∠E=（ ）
如图，延长正方形ABCD的边CB到E，使BE=AC，则∠E=（ ）| A． | 15° | B． | 22.5° | C． | 30° | D． | 45° |