题目内容
15. 如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为$(\sqrt{2},\sqrt{2})$,点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值为( )
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为$(\sqrt{2},\sqrt{2})$,点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 作A关于OB的对称点D,连接CD交OB于P,连接AP,则此时PA+PC的值最小,根据勾股定理求出CD,即可得出答案.
解答  解:作A关于OB的对称点D,连接CD交OB于P,连接AP,则此时PA+PC的值最小,
解:作A关于OB的对称点D,连接CD交OB于P,连接AP,则此时PA+PC的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵B$(\sqrt{2},\sqrt{2})$,
∴AB=$\sqrt{2}$,OA=$\sqrt{2}$,
∵∠OAB=90°,
∴∠B=∠AOB=45°,
由勾股定理得:OB=AD=2,
∵C(1,0),
∴CD=$\sqrt{3}$,
即PA+PC的最小值是$\sqrt{3}$
故选B.
点评 本题考查了轴对称-最短路线问题,三角形的内角和定理,勾股定理,关键是求出P点的位置,题目比较好,难度适中.

练习册系列答案
相关题目
5. 如图表示的是不等式组( )的解集.
如图表示的是不等式组( )的解集.
 如图表示的是不等式组( )的解集.
如图表示的是不等式组( )的解集.| A. | $\left\{\begin{array}{l}{x≤1}\\{x<-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≤1}\\{x>-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥1}\\{x<-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≥1}\\{x>-2}\end{array}\right.$ |
6.下列运算中,正确的是( )
| A. | 2a-a=1 | B. | a+a=2a | C. | (a3)3=a6 | D. | a8÷a2=a4 |
3.已知单项式-xm-2y3与xny2m-3n是同类项,那么m,n的值分别是( )
| A. | $\left\{\begin{array}{l}{m=3}\\{n=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=3}\\{n=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=-3}\\{n=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=-3}\\{n=-1}\end{array}\right.$ |
10. 如图,在平面直角坐标系xOy中,点A,B,C满足二次函数y=ax2+bx的表达式,则对该二次函数的系数a和b判断正确的是( )
如图,在平面直角坐标系xOy中,点A,B,C满足二次函数y=ax2+bx的表达式,则对该二次函数的系数a和b判断正确的是( )
 如图,在平面直角坐标系xOy中,点A,B,C满足二次函数y=ax2+bx的表达式,则对该二次函数的系数a和b判断正确的是( )
如图,在平面直角坐标系xOy中,点A,B,C满足二次函数y=ax2+bx的表达式,则对该二次函数的系数a和b判断正确的是( )| A. | a>0,b>0 | B. | a<0,b<0 | C. | a>0,b<0 | D. | a<0,b>0 |
20.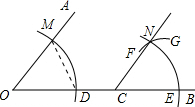 如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
 如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )| A. | 线段OD的长 | B. | 线段OM的长 | C. | 线段DM的长 | D. | 线段CE的长 |
7.由于经济不景气,传统行业产能大幅缩水,某钢厂1月份产量为240万吨,3月份降低到15万吨,则2,3月份平均减产的百分率为( )
| A. | 25% | B. | 75% | C. | -75% | D. | 50% |
4.《孙子算经》中有一道题:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺.”如果设木条长为x尺,绳子长为y尺,根据题意列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+4.5=y}\\{\frac{y}{2}+1=x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=y+4.5}\\{\frac{y}{2}+1=x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=y+4.5}\\{y=\frac{x}{2}+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+4.5=y}\\{x=\frac{y}{2}-1}\end{array}\right.$ |



