题目内容
11. 二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+c>b;②4ac<b2;③2a+b>0.其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+c>b;②4ac<b2;③2a+b>0.其中正确的有( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ② |
分析 分别根据x=-1时y<0和抛物线与x轴的交点、抛物线的对称轴在x=1右侧列式即可得.
解答 解:由图象知,当x=-1时,y=a-b+c<0.即a+c<b,故①错误;
∵抛物线与x轴有2个交点,
∴b2-4ac>0,即4ac<b2,故②正确;
∵抛物线的对称轴x=-$\frac{b}{2a}$>1,且a<0,
∴-b<2a,即2a+b>0,故③正确;
故选:C.
点评 此题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用是解题关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
6.下列运算中,正确的是( )
| A. | 2a-a=1 | B. | a+a=2a | C. | (a3)3=a6 | D. | a8÷a2=a4 |
16.已知两圆的半径分别为1和5,圆心距为4,那么两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
3.已知单项式-xm-2y3与xny2m-3n是同类项,那么m,n的值分别是( )
| A. | $\left\{\begin{array}{l}{m=3}\\{n=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=3}\\{n=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=-3}\\{n=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=-3}\\{n=-1}\end{array}\right.$ |
20.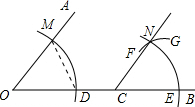 如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
 如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )| A. | 线段OD的长 | B. | 线段OM的长 | C. | 线段DM的长 | D. | 线段CE的长 |
1.下列算式可用平方差公式计算的是( )
| A. | (3m-n)(-3m+n) | B. | (-a+b)(-a-b) | C. | (-a-b)(a+b) | D. | (2a+b)(2b-a) |
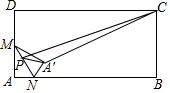 如图,在矩形ABCD中,AB=4,AD=2,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C.在MN上存在一动点P.连接A'P、CP,则△A'PC周长的最小值是$\sqrt{17}$-1+2$\sqrt{5}$.
如图,在矩形ABCD中,AB=4,AD=2,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C.在MN上存在一动点P.连接A'P、CP,则△A'PC周长的最小值是$\sqrt{17}$-1+2$\sqrt{5}$.