题目内容
18.解方程:(1)$\frac{x}{x+1}$-$\frac{4}{{x}^{2}-1}$=1
(2)$\frac{5x-4}{x-2}$=$\frac{4x+10}{3x-6}$-1.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:x(x-1)-4=x2-1,
整理得:x2-x-4=x2-1,
解得:x=-3,
经检验x=-3是分式方程的解;
(2)去分母得:15x-12=4x+10-3x+6,
解得:x=2,
经检验x=2是增根,原方程无解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程时注意不要忘了检验.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
9.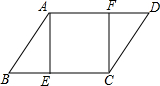 如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )
如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )
 如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )
如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )| A. | 18 | B. | 24$\sqrt{2}$ | C. | 24 | D. | 24$\sqrt{3}$ |
3.下列各式由左到右的变形中,属于因式分解的是( )
| A. | (x+2)(x-1)=x2+x-2 | B. | x2+x+1=(x+1)2-x | ||
| C. | -a2-ab-ac=-a(a+b+c ) | D. | a2+b2=(a+b)2-2ab |
10.分式方程$\frac{2}{x}$=$\frac{3}{x+2}$的解为( )
| A. | x=4 | B. | x=3 | C. | x=2 | D. | x=1 |
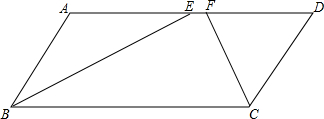 如图,在平行四边形ABCD中,∠ABC的平分线BE交边AD于点E,∠BCD的平分线CF交边AD于点F.求证:AF=DE.
如图,在平行四边形ABCD中,∠ABC的平分线BE交边AD于点E,∠BCD的平分线CF交边AD于点F.求证:AF=DE.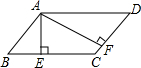 已知?ABCD的周长为64cm,BC边上的高AE=6cm,CD边上的高AF=10cm,求S?ABCD.
已知?ABCD的周长为64cm,BC边上的高AE=6cm,CD边上的高AF=10cm,求S?ABCD.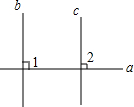 如图,已知a⊥b,a⊥c,求证:b∥c.
如图,已知a⊥b,a⊥c,求证:b∥c.