题目内容
19.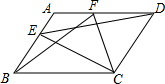 如图,在平行四边形ABCD中,点E是AB边上一点,点F是AD边上一点,试说明S△ECD=S△FBC的理由.
如图,在平行四边形ABCD中,点E是AB边上一点,点F是AD边上一点,试说明S△ECD=S△FBC的理由.
分析 延长DC,过F作FM⊥BC,过E作EN⊥DC,根据平行四边形的面积公式可得S平行四边形ABCD=BC•FM=CD•EN,△BFC和△CDE的面积,可得这两个三角形的面积都是平行四边形面积的一半,因此可得结论.
解答 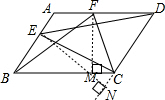 证明:延长DC,过F作FM⊥BC,过E作EN⊥DC,
证明:延长DC,过F作FM⊥BC,过E作EN⊥DC,
∵S平行四边形ABCD=BC•FM=CD•EN,
∴BC•FM=CD•EN,
∵S△BFC=$\frac{1}{2}$CB•FM,S△ECD=$\frac{1}{2}•$CD•EN,
∴S△ECD=S△FBC.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形的面积公式:底×高.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.为了减少燃煤对大气的污染,北京实施煤改电工程.每年冬季采暖季期间可压减燃煤约608000吨,将608000用科学记数法表示应为( )
| A. | 60.8×104 | B. | 6.08×104 | C. | 0.608×106 | D. | 6.08×105 |
9.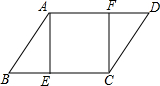 如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )
如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )
 如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )
如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )| A. | 18 | B. | 24$\sqrt{2}$ | C. | 24 | D. | 24$\sqrt{3}$ |
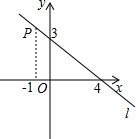 如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;
如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;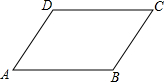 如图所示,∠A+∠C=80°,?ABCD的周长为40cm,且AB-BC=2cm,求?ABCD的各边长和各内角的度数.
如图所示,∠A+∠C=80°,?ABCD的周长为40cm,且AB-BC=2cm,求?ABCD的各边长和各内角的度数.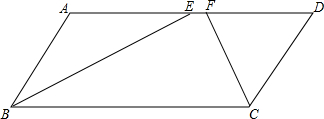 如图,在平行四边形ABCD中,∠ABC的平分线BE交边AD于点E,∠BCD的平分线CF交边AD于点F.求证:AF=DE.
如图,在平行四边形ABCD中,∠ABC的平分线BE交边AD于点E,∠BCD的平分线CF交边AD于点F.求证:AF=DE.