题目内容
16.反比例函数y=$\frac{k}{x}$,当自变量x的值从1增加到2,函数值就减少了3,则函数解析式为( )| A. | y=$\frac{3}{x}$ | B. | y=$\frac{2}{x}$ | C. | y=$\frac{6}{x}$ | D. | y=3x |
分析 先计算出自变量为1和2的函数值,再根据函数值相差3得到k-$\frac{k}{2}$=3,然后解此方程求出k即可得到反比例函数解析式.
解答 解:当x=1时,y=k;当x=2时,y=$\frac{k}{2}$;
根据题意,k-$\frac{k}{2}$=3,
解得:k=6.
所以反比例函数解析式为y=$\frac{6}{x}$.
故选:C.
点评 本题考查了用待定系数法求反比例函数解析式:(1)设出含有待定系数的反比例函数解析式y=$\frac{k}{x}$(k为常数,k≠0);(2)把已知条件(自变量与函数的对应值)代入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
5.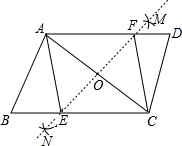 如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )
如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )
 如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )
如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )| A. | AE=AF | B. | AC=EF | C. | ∠EAF=90° | D. | ∠AFE=45° |
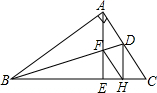 已知,如图,在Rt△ABC中,∠A=90°,AE是高,BD是∠ABC的平分线,AE与BD相交于点F,DH⊥BC,垂足为H,求证:四边形AFHD是菱形.
已知,如图,在Rt△ABC中,∠A=90°,AE是高,BD是∠ABC的平分线,AE与BD相交于点F,DH⊥BC,垂足为H,求证:四边形AFHD是菱形.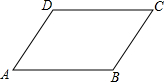 如图所示,∠A+∠C=80°,?ABCD的周长为40cm,且AB-BC=2cm,求?ABCD的各边长和各内角的度数.
如图所示,∠A+∠C=80°,?ABCD的周长为40cm,且AB-BC=2cm,求?ABCD的各边长和各内角的度数.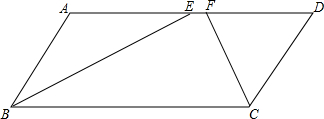 如图,在平行四边形ABCD中,∠ABC的平分线BE交边AD于点E,∠BCD的平分线CF交边AD于点F.求证:AF=DE.
如图,在平行四边形ABCD中,∠ABC的平分线BE交边AD于点E,∠BCD的平分线CF交边AD于点F.求证:AF=DE.