题目内容
16.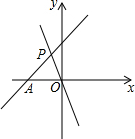 如图,直线y=x+3交x轴于A,与直线y=kx交于点P,且S△AOP=3,求关于x的不等式0<kx<x+3的解集.
如图,直线y=x+3交x轴于A,与直线y=kx交于点P,且S△AOP=3,求关于x的不等式0<kx<x+3的解集.
分析 先利用x轴上点的坐标特征确定A点坐标,再利用三角形面积公式确定P点坐标,然后观察函数图象,写出在y轴左侧且直线y=x+3在直线y=kx上方所对应的自变量的范围即可.
解答 解:当y=0时,x+3=0,解得x=-3,则A(-3,0),
设P(t,t+3),
因为S△AOP=3,
所以$\frac{1}{2}$•3•(t+3)=3,解得t=-1,则P(-1,2),
所以当-1<x<0时,0<kx<x+3,
即关于x的不等式0<kx<x+3的解集为-1<x<0.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
7.为了减少燃煤对大气的污染,北京实施煤改电工程.每年冬季采暖季期间可压减燃煤约608000吨,将608000用科学记数法表示应为( )
| A. | 60.8×104 | B. | 6.08×104 | C. | 0.608×106 | D. | 6.08×105 |
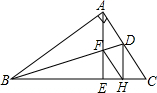 已知,如图,在Rt△ABC中,∠A=90°,AE是高,BD是∠ABC的平分线,AE与BD相交于点F,DH⊥BC,垂足为H,求证:四边形AFHD是菱形.
已知,如图,在Rt△ABC中,∠A=90°,AE是高,BD是∠ABC的平分线,AE与BD相交于点F,DH⊥BC,垂足为H,求证:四边形AFHD是菱形.
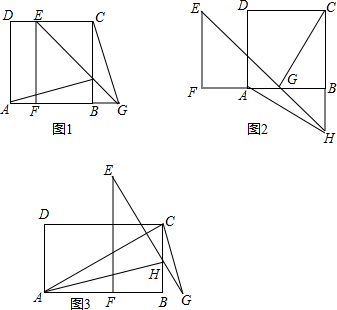
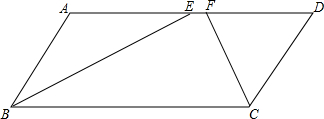 如图,在平行四边形ABCD中,∠ABC的平分线BE交边AD于点E,∠BCD的平分线CF交边AD于点F.求证:AF=DE.
如图,在平行四边形ABCD中,∠ABC的平分线BE交边AD于点E,∠BCD的平分线CF交边AD于点F.求证:AF=DE.