题目内容
3.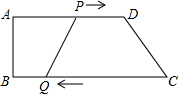 如图1,四边形ABCD中,AD∥BC,∠B=90°,AD=18,BC=21.点P从A出发沿AD以每秒1个单位的速度向点D匀速移动,点Q从点C沿CB以每秒2个单位的速度向点B匀速移动.点P、Q同时出发,其中一个点到终点时两点停止运动,设移动的时间为t秒.求:
如图1,四边形ABCD中,AD∥BC,∠B=90°,AD=18,BC=21.点P从A出发沿AD以每秒1个单位的速度向点D匀速移动,点Q从点C沿CB以每秒2个单位的速度向点B匀速移动.点P、Q同时出发,其中一个点到终点时两点停止运动,设移动的时间为t秒.求:(1)当AB=8时,设A、B、Q、P四点构成的图形的面积为S,求出S关于t的函数关系式,并写出定义域;
(2)点P、点Q与四边形ABCD的任意两个顶点能否构成平行四边形?若能,求出t的值;若不能,说明理由.
分析 (1)A、B、Q、P四点构成的图形是梯形,根据图形的面积公式进行列式计算,即可得到S关于t的函数关系式,容易得出定义域;
(2)分三种情况讨论,分别求出t的值即可.
解答 解:(1)由题得,AP=t,CQ=2t,BQ=21-2t,AB=10,∠B=90°
∴A、B、Q、P四点构成的图形的面积=$\frac{1}{2}$×(AP+BQ)×AB
∴S=,$\frac{1}{2}$×(t+21-2t)×8=-4t+84,
即S═-4t+84,
∵18÷1=18,21÷2=10.5
∴定义域为:0≤t≤10.5;
(2)能构成平行四边形;
当 四边形ABQP为平行四边形时,AP=BQ,
即t=21-2 t,
解得:t=7;
当四边形 PQCD为平行四边形时,PD=CQ,
即2t=18-t,
解得:t=6;
当四边形 BQDP为平行四边形时,PD=BQ,
即18-t=21-2 t,
解得:t=3;
当四边形 AQCP为平行四边形时,AP=CQ,
即t=2t,
解得:t=0,不合题意,舍去;
综上所述:点P、点Q与四边形ABCD的任意两个顶点能构成平行四边形,t的值为7s或6s或3s.
点评 本题是四边形综合题目,考查了梯形的性质、平行四边形的性质以及梯形面积的计算、分类讨论等知识;熟练掌握平行四边形的性质,进行分类讨论是解决问题(2)的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
13.定义运算a?b=a(1-b),下面给出的关于这种运算的结论中正确的是( )
| A. | 2?(-2)=-4 | B. | a?b=b?a | C. | 若a?b=0,则a=0 | D. | (-2)?2=2 |
8.为了保护生态平衡,绿化环境,国家大力鼓励“退耕还林、还草”,其补偿政策如表(一):某农户承包了一片山坡地种树种草,所得到的国家的补偿如表(二).
表(一)种树、种草每亩每年补粮补钱情况表
表(二)该农户收到乡政府下发的当种树种草亩数及年补偿通知单
(1)该农户当年种树、种草各多少亩?
(2)若今年该农户又扩展40亩山坡地种树种草,要想年终政府补钱不少于12000元,至少需要安排多少亩山坡地种树?
表(一)种树、种草每亩每年补粮补钱情况表
| 种树 | 种草 | |
| 补粮 | 150千克 | 100千克 |
| 补钱 | 200元 | 150元 |
| 种树、种草 | 补粮 | 补钱 |
| 30亩 | 4000千克 | 5500元 |
(2)若今年该农户又扩展40亩山坡地种树种草,要想年终政府补钱不少于12000元,至少需要安排多少亩山坡地种树?
 已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点.
已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点.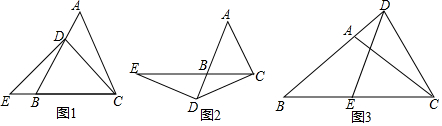
 在5×5的正方形网格中,每个小正方形的边长为1,用四边形覆盖如图所示,被覆盖的网格线中,竖直部分的线段的长度之和记作m,水平部分的线段的长度之和记作n,则m-n=( )
在5×5的正方形网格中,每个小正方形的边长为1,用四边形覆盖如图所示,被覆盖的网格线中,竖直部分的线段的长度之和记作m,水平部分的线段的长度之和记作n,则m-n=( )