题目内容
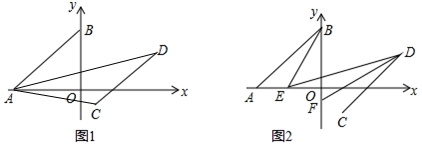
18. 已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点.
已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点.(1)求证:点D在⊙O上;
(2)求证:F是AB的中点;
(3)若DE=4,求⊙O的半径和△BFH的面积.
分析 (1)根据矩形的对角线相等且平分的性质得:OA=OD,所以点D在⊙O上;
(2)证明△AEF≌△BGF,则AF=BF;
(3)先在Rt△OED中,由勾股定理求⊙O的半径为3$\sqrt{2}$;再利用勾股定理计算AD=$\sqrt{{4}^{2}+(2\sqrt{2})^{2}}$=2$\sqrt{6}$,
AB=$\sqrt{(6\sqrt{2})^{2}-(2\sqrt{6})^{2}}$=4$\sqrt{3}$,证明△AFD≌△BFH,可得S△BFH=$\frac{1}{2}$BF•BH,代入计算即可.
解答  证明:(1)∵四边形ABCD是矩形,
证明:(1)∵四边形ABCD是矩形,
∴AO=OC=OD=OB,
∵以O为圆心,OA长为半径作⊙O,
∴点D在⊙O上;
(2)同理,点B也是⊙O上,
连接BG,
∵∠BAD=90°,
∴BD也是直径,
∴∠BGD=90°,
∵BK⊥AC,BK∥DH,
∴∠GEK=90°,
∴BG∥AC,
∴∠FAE=∠FBG,
∵F是EG的中点,
∴EF=FG,
∵∠AFE=∠BFG,
∴△AEF≌△BGF,
∴AF=BF,
∴F是AB的中点;
(3)由(2)得:△AEF≌△BGF,
∴AE=BG,
∵OE⊥DG,
∴DE=EG=4,
∵OB=OD,
∴OE是△DGB的中位线,
∴OE=$\frac{1}{2}$BG,
∴OE=$\frac{1}{2}$AE,
设OE=x,则AE=2x,
∴OD=3x,
在Rt△OED中,由勾股定理得:OE2+ED2=OD2,
∴x2+42=(3x)2,
x=$±\sqrt{2}$,
∴OD=3$\sqrt{2}$,即⊙O的半径为3$\sqrt{2}$;
Rt△AED中,AE=2$\sqrt{2}$,ED=4,
∴AD=$\sqrt{{4}^{2}+(2\sqrt{2})^{2}}$=2$\sqrt{6}$,
Rt△ABD中,BD=2OD=6$\sqrt{2}$,
AB=$\sqrt{(6\sqrt{2})^{2}-(2\sqrt{6})^{2}}$=4$\sqrt{3}$,
∵AF=BF,∠AFD=∠BFH,∠DAF=∠ABH=90°,
∴△AFD≌△BFH,
∴BH=AD=2$\sqrt{6}$,
BF=AF=$\frac{1}{2}$AB=2$\sqrt{3}$,
∴S△BFH=$\frac{1}{2}$BF•BH=$\frac{1}{2}$×$2\sqrt{3}×2\sqrt{6}$=6$\sqrt{2}$.
点评 本题是圆的综合题,考查了全等三角形的性质和判定、矩形的性质、三角形中位线的性质、勾股定理等知识点,难度适中,本题多次运用勾股定理计算线段的长.

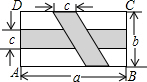 如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形,依照图中标注的数据,计算图中空白部分的面积,其面积是( )
如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形,依照图中标注的数据,计算图中空白部分的面积,其面积是( )| A. | bc-ab+ac+c2 | B. | a2+ab+bc-ac | C. | ab-bc-ac+c2 | D. | bc-ab+ac+c2 |
| A. | 2016x | B. | x+2016 | C. | |2016x| | D. | |x|+2016 |
| A. | x=$\frac{2}{3}$y-10 | B. | x=$\frac{2}{3}$y+10 | C. | y=$\frac{3}{2}$x-15 | D. | y=$\frac{3}{2}$y+15 |
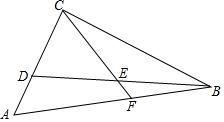 已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A.
已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A.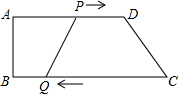 如图1,四边形ABCD中,AD∥BC,∠B=90°,AD=18,BC=21.点P从A出发沿AD以每秒1个单位的速度向点D匀速移动,点Q从点C沿CB以每秒2个单位的速度向点B匀速移动.点P、Q同时出发,其中一个点到终点时两点停止运动,设移动的时间为t秒.求:
如图1,四边形ABCD中,AD∥BC,∠B=90°,AD=18,BC=21.点P从A出发沿AD以每秒1个单位的速度向点D匀速移动,点Q从点C沿CB以每秒2个单位的速度向点B匀速移动.点P、Q同时出发,其中一个点到终点时两点停止运动,设移动的时间为t秒.求: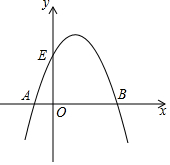 已知抛物线经过点A(-1,0),B(3,0),C(1,4),与y轴交于点E.
已知抛物线经过点A(-1,0),B(3,0),C(1,4),与y轴交于点E.